About unique determination of symmetric point (or center) of a distribution based on pdf or cdf

Question

Suppose we have a distribution that is known to be continuous and symmetric, and is otherwise unknown. We want to decide whether it is actually centered at zero using an equation involving pdf or cdf. We are only allowed to use a subset of the support of this symmetric distribution.

To fix ideas, suppose $X$ is a continuous and symmetric random variable with pdf $f(\cdot)$, cdf $F(\cdot)$ and support $\mathcal{X}$. Suppose $B$ is a subset of $\mathcal{X}$. One way to go is to use equations involving pdf, i.e., we ask does $f(x)=f(-x+a)$ for $x\in B$ imply $a=0$? For this "test" to work, one obvious case to rule out is $f(\cdot)$ being the pdf of a uniform distribution. The counterexample: if the underlying true distribution is the uniform distribution on $\mathcal{X}=[-1,1]$, and suppose $B=[-0.5,0]$, then obviously $f(x)=f(-x+a)$ do not imply $a=0$. To see this, take $a=0.1$, then $f(x)=f(-x+0.1)$ for any $x\in B$ even though $a\neq 0$.

Thus, at least for $f(x)=f(-x+a)$ for $x\in B$ to imply $a=0$, the distribution $f(\cdot)$ cannot be a uniform distribution.

However, I guess if we use the cdf equation $F(x)=1-F(-x+a)$, then $F(x)=1-F(-x+a)$ for any $x\in B$ will imply $a=0$, even if $F(\cdot)$ is the cdf of a uniform distribution. To see this, we can use the previous counterexample, which is no longer a problem here. If the true distribution is uniform, $F(x)=1-F(-x+a)$ translates to $\frac{t+1}{2}=1-\frac{-t+a+1}{2}$, which implies $a=0 $. My question is: does this look correct? If yes, what's the intuition behind it? Can you think of some counterexamples such that this cdf approach do not imply $a=0$? Thanks!

Answer 1

The question concerns how much information about a symmetric (cumulative) distribution function $F$ is needed to determine its center of symmetry. Specifically, when $x$ and $y$ are numbers for which

$$F(y) = 1 - F(x),$$

and $F$ is continuous at $x$ and $y,$ we might guess that the center of symmetry is

$$a = (y + x)/2.$$

However, this fails for bounded distributions because when $y$ is less than the lower bound and $x$ is greater than the upper bound, $F(y)=0 = 1-1 = 1 - F(x),$ but that gives no information about the center of $F.$ The question implicitly recognizes this problem by requiring $x$ and $y$ to be in the support of $F:$ that would rule out such trivialities.

The situation may be subtler than it looks. In particular, it is possible that even infinitely many equations of the form $F(y)=1-F(x),$ where $x$ and $y$ are in the support of $F,$ will not suffice to determine the center of $F.$

How this can happen is revealing. I will construct and analyze an example. But first, because of the subtleties, let us review the relevant definitions.

Definitions and Terms

A symmetric random variable $X$ "behaves like its negative" in the sense that (a) there is a number $a,$ a "center of symmetry," for which (b) the variables $Y=X-a$ and $-Y=a-X$ have identical distributions. In terms of the law of $X$ (its cumulative distribution function $F$), this means the functions $F$ and $x\to 1-F(-x)$ are "nearly" the same. (They will differ wherever $F$ has a jump.) To simplify the discussion, from now on I will assume $F$ is continuous (it has no discrete jumps).

When $F$ is symmetric, its center $a$ is uniquely determined.

The support of a random variable (and therefore, by extension, of its distribution function) is the smallest closed set on which the variable has probability $1.$ For instance, the support of the uniform distribution on the open interval $(0,1)$ is the closed interval $[0,1].$

When $x$ and $y$ are in the support of a distribution $F$ and $F(y) = 1 - F(x),$ let us say that $(x+y)/2$ is a candidate for the center of $F.$

An Example

I will invite you to build a distribution with positive support by shifting some basic distributions out to various positive locations and then symmetrizing that around $0.$ You may freely choose these basic distributions, but if you want to follow the construction with a truly concrete example, take them all to be the uniform distribution on $[0,1].$

Let $p_0,p_1,p_2,\ldots$ be a sequence of positive numbers that sums to unity. These will serve as weights in a mixture distribution. Let $q_0, q_1, q_2, \ldots$ be any sequence of positive numbers. Let the partial sums of the sequence $(1+2q_i)$ be $$x_0=0 \lt x_1=1+2q_0 \lt x_2=2+2(q_0+q_1) \lt x_3=3+2(q_0+q_1+q_2)\lt \cdots$$

The $x_i$ will determine the positions of the mixture components. Finally, let $F_0,F_1,F_2,\ldots$ be a sequence of (continuous) distribution functions all of which have the interval $[0,1]$ for their support.

Shift distribution $F_i$ to the interval $[x_{i},x_{i}+1].$ This defines the distribution functions

$$G_i(x) = F_i(x - x_i).$$

Notice that all the intervals $[x_i, x_i+1]$ are disjoint with gaps of $x_{i+1}-(x_i+1) = 1+2q_i-1 = 2q_i \gt 0$ between interval $i$ and interval $i+1.$

The mixture of these shifted, scaled distributions is the distribution function

$$G(x) = \sum_{i=0} p_i G_i(x).$$

Finally, symmetrize $G$ around $a=0$ by setting

$$F(x) = \frac{1 + \operatorname{sgn}(x)G(|x|)}{2} = \left\{\begin{aligned}\frac{1+G(x)}{2},&\ x \ge 0\\\frac{1-G(-x)}{2},&\ x \lt 0.\end{aligned}\right.$$

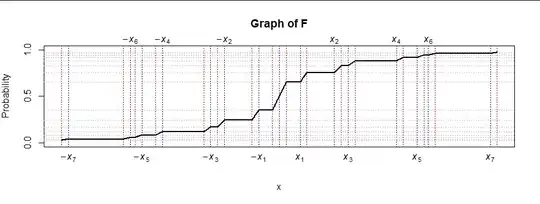
In this illustration, the left endpoints of the intervals at $x_i$ are shown in blue and the right endpoints at $x_i+1$ are shown in red. This is then reflected around the origin at $x_0=0.$ $F$ is flat between successive intervals.

This plot of the density $f$ of $F$ helps show how the basic uniform distributions have been shifted and weighted symmetrically, making it clear there really is a unique center:

Analysis of the Example

By construction, the support of $F$ is the union of all intervals

$$\cdots \cup [-x_{2}-1, -x_{2}] \cup [-x_{1}-1, -x_1] \cup [-1,0] \cup [0, 1] \cup [x_1,x_1+1] \cup [x_2,x_2+1] \cup \cdots.$$

For each $i=1,2,3,\ldots,$ $x_{i}$ is in the support: it is the left hand endpoint of the interval $[x_{i}, x_{i}+1].$

Because $F$ is continuous and has no probability in the gap from $x_i+i$ to $x_{i+1},$ it has the same values at those points; and because it is symmetric about $0,$ we find

$$F(-x_{i+1}) = F(-x_i-1) = 1 - F(x_i+1) = 1 - F(x_{i+1}).$$

The question hopes we can determine the center of $F$ from relationships such as these. For instance, the equality $F(-x_{i+1}) = 1-F(x_{i+1})$ would suggest the center is

$$a = (x_{i+1} + -x_{i+1})/2 = 0,$$

which would be correct. However, applying the same reasoning to the equality $F(-x_i-1) = 1 - F(x_{i+1})$ would then imply

$$a = (x_{i+1} + -x_i - 1)/2 = q_i$$

(as we computed earlier). A similar calculation suggests $a = -q_i$ is also a candidate.

Consequently, along with $0,$

Every one of the $\pm q_i$ is a candidate (potential center) of $F$!

How awful can this get? Let $\left[\ \right]$ denote rounding a number to the nearest integer. Define the functions

$$m(i) = \left[\sqrt{2i}\right];\ b(i) = i - \binom{m(i)}{2};\ a(i)=m(i)+1-b(i)$$

and set

$$q(i) = a(i)/b(i),\ i=1,2,3,\ldots.$$

These constitute all the rational numbers:

$$\{q(i), i=1,2,3,\ldots\} \cup \{-q(i), i=1,2,3,\ldots\} \cup\{0\} = \mathbb{Q}.$$

(Proof: We need to show every positive rational number $q$ appears in the sequence $(q_i).$ Write $q=a/b$ where $a$ and $b$ are positive integers. Set $m=a+b-1$ and $i=b + \binom{m}{2}$ and calculate that $a=a(i)$ and $b=b(i).$ Therefore, $q = q_i,$ QED.)

In other words,

Every real number is arbitrarily close to a candidate for this $F.$

---

What is the resolution of the problem illustrated by this example? One is to insist on using only equations of the form $F(y) = 1 - F(x)$ when $F$ assigns positive probability to all neighborhoods of at least one of $x$ and $y.$ In such a case it is straightforward to show that $a = (x+y)/2$ truly is the center of $F$ (provided $F$ is symmetric about some center).