Representing experimental data

Question

I have an argument with my advisor over data visualization. He claims that when representing experimental results, the values should be plotted with "markers" only, as presented in the image bellow. While curves should only represent a "model"

I on the other hand believe that a curve is unnecessary in many cases in order to facilitated readability, as shown in the second image bellow:

Am I wrong or my professor? If the later one is the case, how do I go around to explain this to him.

Answer 1

As JeffE says: the points are the data. In general, it's good to avoid adding curves as much as possible. One reason for adding curve is that it makes the graph nicer to the eye, by making the points and the trend between the points more readable. This is particularly true if you have few data points.

However, there are other ways to display sparse data, that may be better than a scatter plot. One possibility is a bar chart, where the various bars are much more visible than your single points. A color code (similar to what you already have in your figure) will help see the trends in each data series (or the data series could be split, and presented next to each other in smaller individual bar charts).

Finally, if you really want to add some sort of line between your symbols, there are two cases:

1. If you expect a certain model to be valid for your data (linear, harmonic, whatever), you should fit your data on the model, explain the model in the text and comment on the agreement between data and model.

2. If you do not have any reasonable model for the data, you should not include extra assumptions in your graph. In particular, this means you should not include any type of lines between your points except strait lines. The nice “spline fit” interpolations that Excel (and other software) can draw are a lie. There is no valid reason for your data to follow that particular mathematical model, so you should stick to straight line segments.

   Furthermore, in that case it can be nice to add a disclaimer somewhere in the figure caption, like “lines are only guides for the eye”.

Answer 2

I like this rule of thumb:

If you need the line to guide the eye (i.e. to show a trend that without the line would not be visible as clearly), you should not put the line.

Humans are extremely good at recognizing patterns (we're rather on the side of seeing trends that do not exist than missing an existing trend). If we are not able to get the trend without line, we can be pretty sure that no trend can be conclusively shown in the data set.

Talking about the second graph, the only indication of the uncertainty of your measurement points are the two red squares of C:O 1.2 at 700 °C. The spread of these two means that I would not accept e.g.

• that there is a trend at all for C:O 1.2
• that there is a difference between 2.0 and 3.6
• and for sure the curved models are overfitting the data.

without very good reasons given. That, however, would again be a model.

---

edit: answer to Ivan's comment:

I'm chemist and I'd say that there is no measurement without error - what is acceptable will depend on the experiment and instrument.

This answer is not against showing experimental error but all for showing and taking it into account.

The idea behind my reasoning is that the graph shows exactly one repeated measurement, so when the discussion is how complex a model should be fit (i.e. horizontal line, straight line, quadratic, ...) this can give us an idea of the measurement error. In your case, this means that you would not be able to fit a meaningful quadratic (spline), even if you had a hard model (e.g. thermodynamic or kinetic equation) suggesting that it should be quadratic - you just don't have enough data.

To illustrate this:

df <-data.frame (T      =         c ( 700,  700,  800, 900,  700, 800, 900, 700, 800, 900), 
                 C.to.O = factor (c ( 1.2,  1.2,  1.2, 1.2,  2  , 2  , 2  , 3.6, 3.6, 3.6)),
                 tar    =         c (21.5, 18.5, 19.5, 19,  15.5, 15 , 6  , 16.5, 9, 9))

Here's a linear fit together with its 95% confidence interval for each of the C:O ratios:

ggplot (df, aes (x = T, y = tar, col = C.to.O)) + geom_point () + 
    stat_smooth (method = "lm") + 
    facet_wrap (~C.to.O)

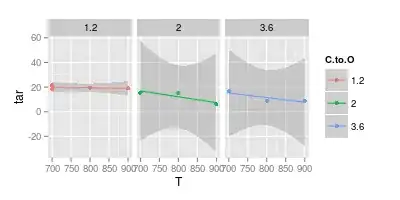
Note that for the higher C:O ratios the confidence interval ranges far below 0. This means that the implicit assumptions of the linear model are wrong. However, you can conclude that the linear models for the higher C:O contents are already overfit.

So, stepping back and fitting a constant value only (i.e. no T dependence):

ggplot (df, aes (x = T, y = tar, col = C.to.O)) + geom_point () + 
    stat_smooth (method = "lm", formula = y ~ 1) + 
    facet_wrap (~C.to.O) 

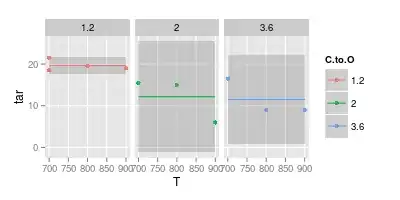
The complement is to model no dependence on C:O:

ggplot (df, aes (x = T, y = tar)) + geom_point (aes (col = C.to.O)) + 
    stat_smooth (method = "lm", formula = y ~ x) 

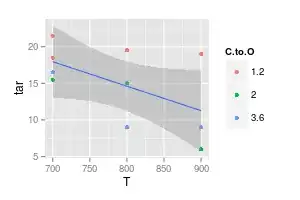
Still, the confidence interval would cover a horizontal or even slightly ascending lines.

You could go on and try e.g. allowing different offsets for the three C:O ratios, but using equal slopes.

However, already few more measurements would drastically improve the situation - note how much narrower the confidence intervals for C:O = 1 : 1 are, where you have 4 measurements instead of only 3.

Conclusion: if you compare my points of which conclusions I'd be sceptical of, they were reading way too much into the few available points!

Answer 3

1-Your professor is making a valid point.

2-Your plot definitely does not increase readability IMHO.

3-From my understanding this is not the right forum to ask this sort of a question really and you should ask it at cross-validated.

Answer 4

Sometimes joining points makes sense, especially if they are very dense.

And then it may make sense to interpolate (e.g. with a spline). However, if it is anything more advanced than spline of order one (for which it is visibly obvious that it is just joining points), you need to mention it.

However, for the case of a few points, or a dozen, points, it is not the case. Just leave the points as they are, with markers. If you want to fit a line (or another curve), it is a model. You can do add it, but be explicit - e.g. "line represents linear regression fit".

Answer 5

I think there are cases where one is not proposing an explicit model, yet needs some kind of guide to the eye. My rule then is to avoid curves like the plague and stick to piecewise straight lines between successive points of a series.

For one, this assumption is more obvious to readers. Also the spikiness is good at keeping readers away from assuming trends unsupported by data. If at all, this only highlights noise and outliers.

The stuff I'm wary of is cursory (non-rigorous, non-explicit) use of splines, quadratics, regression etc. Very often this makes it seem there are trends where there are none. A good example of abuse are the curves drawn by @Ivan. With 3 datapoints I don't think any maxima or minima in the underlying model are obvious.