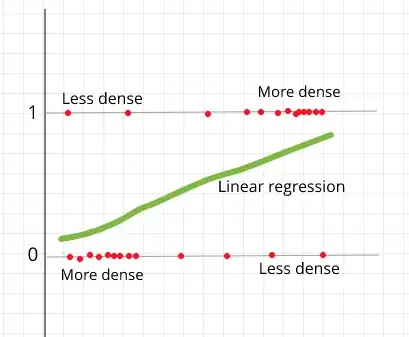
This is less a question about sklearn's implementation, and more theoretical. I find it weird that we'd do isotonic regression against target values in {0, 1} because that could result in very jagged results. Why not use the calibration curve to do the calibration?
So to give you an example, I had a binary classification problem which was imbalanced towards 95% probability of a positive. I trained it on rebalanced data and tried validating it on unbalanced data. Of course that didn't turn out so great, so I went for calibration via isotonic regression.
So here's the "normal" way of doing it:
def predict_via_isotonic_calibration(y_true, y_prob):
"""
y_true is an array of binary targets
y_prob is an array of predicted probabilities from an uncalibrated classifier
"""
iso_reg = IsotonicRegression(out_of_bounds='clip').fit(y_prob, y_true)
calibrated_y_prob = iso_reg.predict(y_prob)
return calibrated_y_prob
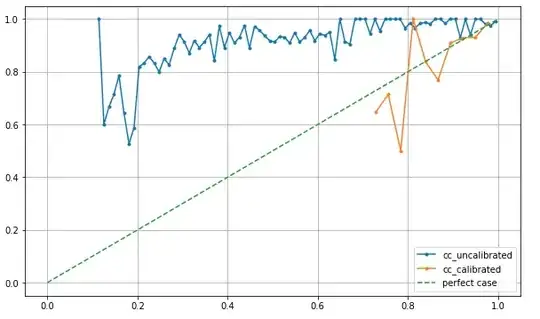
Which gave me this (calibrated vs uncalibrated):
Whereas I think it should be more like:
def predict_via_isotonic_calibration(y_true, y_prob, n_bins=80):
y, x = calibration_curve(y_true, y_prob, n_bins=n_bins)
iso_reg = IsotonicRegression(out_of_bounds='clip').fit(x, y)
calibrated_y_prob = iso_reg.predict(y_prob)
return calibrated_y_prob
Which gave me this much nicer calibration:
So what gives? Is my idea a thing? Or is it wrong for some reason I'm overlooking.