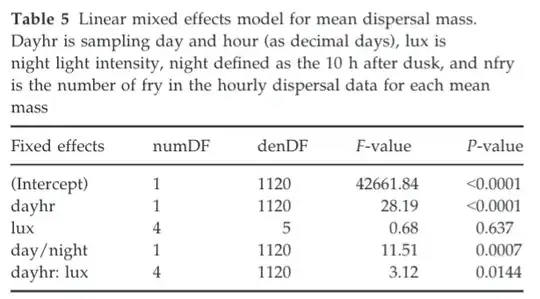
I was reading a paper yeaterday, and in their results they reported an F-score for each of their fixed effects in a linear mixed effect model.
Here, lux is a catagorical variable, but the rest are continuous. I haven't come across this before. Normally, I'm used to seeing Z or T scores, and these represent Wald tests --- examining the the regression slope for a given predictor variable is significantly different than 0.
Can someone explain to me:
- What is the F-statistic testing in this context?
- How are the numerator and denominator degrees of freedom calculated in this context (just in a GLM sense, we don't have to worry about the issues that come along with mixed models here if there are some).
- And finally, if its not implicitly answered in the first point... why would an author opt to do hypothesis testing with F scores, rather than Z or T scores.
My first intuition was that perhaps all the variables were categorical, so this is just an ANOVA... but I'm quite sure most of the variables are not categorical here.
Reference
Riley, W. D., Davison, P. I., Maxwell, D. L., Newman, R. C. and Ives, M. J. (2015). A laboratory experiment to determine the dispersal response of Atlantic salmon (Salmo salar) fry to street light intensity. Freshwater Biol 60, 1016–1028.