0

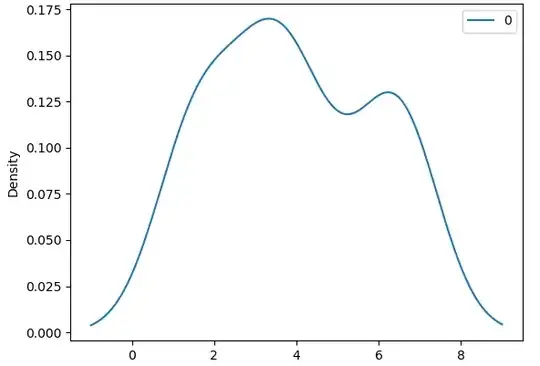
I've come across a stats problem while working on my thesis. I ran multiple t-tests on a series of environmental parameters to determine if two groups of data are different (eg, early years vs. late years of data, urbanized vs. non-urbanized habitats). I used Welch's t-test in R to test these hypotheses, but it was later brought to my attention that t-tests should only be performed on normally distributed data (most of my data is not). I included a histogram from my dataset which resembles a lot of my data as example below. I experimented with log-transformations, which helped in some cases but most of my data is still non-normal. Fortunately, I have a large sample size (N = 865) which I understand allows me to relax some of the assumptions surrounding normality.

My question is:

How do I determine if my sample size is large enough to accept non-normal data? I imagine this is likely a case-by-case determination, but I am running around 150 tests in total so I am looking for a solution that I could automate into my code. And if t-tests are not appropriate, what's the next best alternative?

Thanks!

example histogram

AgnusScythicus
  • 1
  • 1
  • 1
    When in doubt, you can simulate. See https://stats.stackexchange.com/a/69967/919 for a detailed example. – whuber Oct 19 '20 at 20:11

1 Answers1

1

Kohavi et al. [1] proposed a rule of thumb on the number of samples required in experiments on the Web that involves skewness. They suggested (in page 8, section "Rule #7") the minimum number of i.i.d. samples required per group for a good enough (i.e. normal-looking) sample mean is:

$$ 355 \times s^2 , \textrm{where}\, s = \frac{\mathbb{E}\left[(X - \mathbb{E}(X))^3\right]}{(Var(X))^{3/2}}$$ and $X$ is the random variable modelling the sample distribution. There are some nuances that I am not reproducing in this answer but are in the text.

This might sound a relatively large number, but is actually quite easily met in Web experimentation.

Failing that (i.e. meeting the suggested sample size requirements), non-parametric (rank-based) tests, e.g. Mann-Whitney and Kruskal-Wallis, might be viable alternatives depending on your exact hypotheses.

[1] R. Kohavi, A. Deng, R. Longbotham, Y. Xu (2014) Seven Rules of Thumb for Web Site Experimenters. In: KDD'14. New York, NY, USA. https://www.exp-platform.com/Documents/2014%20experimentersRulesOfThumb.pdf

B.Liu
  • 1,025
  • 5
  • 17