3

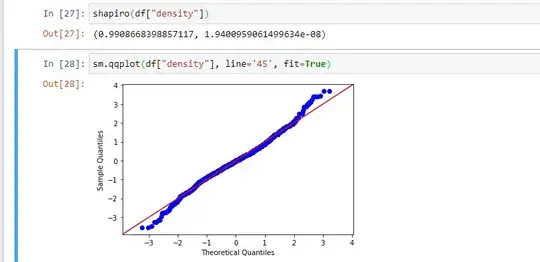
I have a problem comparing results from shapiro test and qqplot. Shapiro tells me my data doesn't have normal distribution characteristics (pvalue = 1.94...e-08 <= 0.05) however when I look on QQ plot the points are pretty close to the reference line.

enter image description here

How should I interpret that?

I'm using shapiro function from: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.shapiro.html

Alienown
  • 33
  • 3
  • 7
    Why do you want to test normality? See [this page](https://stats.stackexchange.com/q/2492/28500) for an introduction to extensive discussion about why strict testing for normality as with the Shapiro test seldom adds much. In practice, with enough data points real-world data will often deviate "significantly" from normal based on such tests, but not to an extent that substantially affects inference. – EdM Oct 18 '20 at 15:43

2 Answers2

10

You seem to have quite a large sample size which is probably why the Shapiro-Wilk test returns a small p-value. In general statistical tests for normality are not a great idea in large part for this very reason.

There is some evidence, from the QQ plot, of slightly heavy tails. However, this is a fairly mild departure and in my opinion you are justified in considering these data to be approximately normally distributed.

I do wonder, however, why you are concerned about whether these data follow a normal distribution.

Robert Long
  • 53,316
  • 10
  • 84
  • 148
4

You should not worry too much about the return of the Shapiro-Wilk test, especially with higher sample sizes this can happen as already mentioned, the Q-Q plot looks fine.

Another option I would like to add is to simply visually inspect the data with a histogram, this can help some times more than a plain number given out by a normality Test.

You could use the histogram function from package numpy: https://numpy.org/doc/stable/reference/generated/numpy.histogram.html#numpy.histogram

and get a result like this:

enter image description here

Ale
  • 1,570
  • 2
  • 10
  • 19
SeppSeppenbauer
  • 43
  • 6