such as find MLE of $P(X>12)$ when $X_i$ ~ $N(\mu,\sigma^2) $
-
Maybe write out $P$ as an integral and try to derive the likelihood function. I’m curious where this goes. +1 – Dave Oct 16 '20 at 12:58
-
1[not sure if I'm correctly interpreting the question] The higher the value of $\mu$, the higher the value of $P(X>12)$, so it seems there would be no finite answer. For a fixed $\mu>12$, the variance should be as small as possible (to approach 1). For a fixed $\mu<12$, the variance should be as large as possible (to approach 0.5) – jpneto Oct 16 '20 at 13:32
-
@jpneto You’ve misinterpreted something about maximum likelihood estimation. Even the maximum likelihood estimator of $\mu$, the usual sample mean $\bar{X}$, has no bounds. – Dave Oct 16 '20 at 13:40
-
1@Dave There appear to be several forms of misinterpretation in this comment thread, so I posted a solution in the hope that might clear things up a little. – whuber Oct 16 '20 at 14:30
-
Perhaps the question should be MLE of $Pr(X>12 | x_1, x_2,...)$. But maybe that was obvious. – Dayne Oct 16 '20 at 15:04
-
1@jpneto P(X>12) should not be as high as possible. The estimate of P(X>12) should be as close as possible to the true value of P(X>12). And you can do that estimation by estimating maximizing the likelihood, but the likelihood is not equal to this P(X>12). The value P(X>12) is the parameter to be optimized. – Sextus Empiricus Oct 16 '20 at 20:10
1 Answers
As I'm sure you know (or can easily derive), the maximum likelihood estimator of $(\mu,\sigma^2)$ is
$$(\hat\mu,\hat\sigma^2) = \left(\bar X, \operatorname{Var}(X)\right)$$
where, as usual, $n\bar X = X_1+X_2+\cdots + X_n$ and, a little unusually,
$$\operatorname{Var}(X) = \frac{1}{n}\left((X_1-\bar X)^2 + (X_2-\bar X)^2 + \cdots + (X_n-\bar X)^2\right)$$
(notice the $n$ rather than the $n-1$ in the denominator).
A fundamental property of MLEs is that a maximum likelihood estimator of any function $f$ of the parameters equals $f$ applied to the MLEs of the parameters. In this case, letting $\Phi$ be the standard Normal CDF
$$f(\mu,\sigma^2) = \Pr(X \gt 12) = 1 - \Phi\left(\frac{12-\mu}{\sqrt{\sigma^2}}\right).$$
Therefore the MLE of $\Pr(X \gt 12)$ is $$\hat f = 1 - \Phi\left(\frac{12-\hat\mu}{\sqrt{\hat\sigma^2}}\right).$$
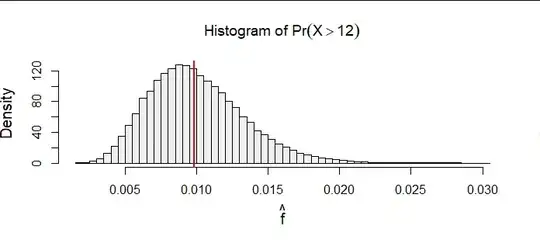
Because maximum likelihood estimation is a procedure intended for relatively large sample sizes, here is a simulation based on 100,000 samples of size $n=240.$ The parameter was set to $(\mu,\sigma)=(5,3).$
You can see how the estimates are spread roughly evenly around the true value (marked as a red vertical segment), indicating this solution is a reasonable estimator. Further simulations with ever larger sample sizes (I went up to $n=24000$ but limited the simulation to just a thousand iterations to keep the computation time down to a second or two) indicate this solution converges around the true value, as it ought.
#
# Specify the problem.
#
mu <- 5
sigma <- 3
threshold <- 12
n <- 240
#
# Draw samples.
#
set.seed(17)
n.sim <- 1e5
x <- matrix(rnorm(n.sim*n, mu, sigma), n.sim)
#
# Compute the MLEs.
#
mu.hat <- rowMeans(x)
sigma2.hat <- rowMeans((x - mu.hat)^2)
p.hat <- pnorm((threshold - mu.hat) / sqrt(sigma2.hat), lower.tail = FALSE)
#
# Plot the MLEs.
#
hist(p.hat, freq=FALSE, col="#f0f0f0", breaks=50,
xlab=expression(hat(f)), cex.lab=1.25,
main=expression(paste("Histogram of ", Pr(X>12))))
abline(v = pnorm(threshold, mu, sigma, lower.tail = FALSE), lwd=2, col="#d01010")
- 281,159
- 54
- 637
- 1,101
-
Small doubt: are we finding here the MLE of the random variable $P \equiv Pr(X>12)$ here? If so, how does the distribution of this random variable (as given in your answer) depends on the observed sample? – Dayne Oct 16 '20 at 14:54
-
@Dayne The probability is not a random variable: it is a number, as always. We are finding the MLE of that number. – whuber Oct 16 '20 at 15:00
-
Yes, my bad. What I meant was that we maximize likelihood function which is interpreted as a function of parameter, given observations. So this function depends on observations. Here the likelihood function didn't seem to be dependent on observations. Anyway, perhaps we are estimating the conditional probability $Pr(X>12 | x_1, x_2,...)$ – Dayne Oct 16 '20 at 15:08
-
@Dayne I'm sorry to keep sounding negative, but that's not what's going on. I didn't write the likelihood function because that's been done in a great many places elsewhere on this site. To try to write it in terms of the parameter $\Pr(X\gt 12)$ (which, I repeat, *is just a number* which we are trying to estimate) would be fruitless (it's hugely complicated) and, as you have seen, unnecessary – whuber Oct 16 '20 at 15:14
-
1Got it. Thanks for comments. Without the conditional part it seemed as the estimate of parameter $Pr(X>12)$ would just be independent of observations, as also alluded by @jpneto. And I agree this method (using the MLE property) is much more elegant. – Dayne Oct 16 '20 at 15:25
-
@whuber re: $Pr(X>12)$ is not a random variable. Sorry, for the inaccurate language, but I am looking for a method to answer questions like "how sure are you that $Pr(X>12)=0.01$ ?" or "how many more samples do you need to be twice sure" - could you give me an hint about what theory I should study? – elemolotiv Feb 28 '21 at 17:18
-
2@elemolotiv When $X$ is a random variable, $\Pr(X\gt 12)$ is a property of its distribution, usually termed a *parameter.* You describe the problem of *estimating* a parameter and the theory is called *statistical (point) estimation.* One of the classic texts is Lehmann & Casella's [Theory of Point Estimation](https://www.amazon.com/Theory-Point-Estimation-Springer-Statistics/dp/0387985026). – whuber Feb 28 '21 at 17:40