Comparison of entropy and distribution of bytes in compressed/encrypted data

Question

I have some question which occupies myself for a while.

The entropy test is often used to identify encrypted data. The entropy reaches its maximum when the bytes of the analyzed data are distributed uniformely. The entropy test identifies encrypted data, because this data has a uniform distribution - like compressed data, which is classified as encrypted when using the entropy test.

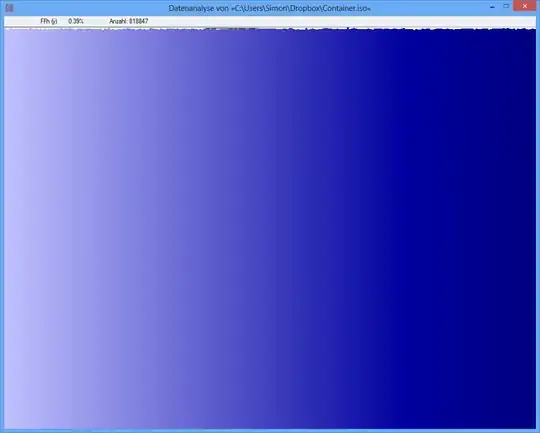
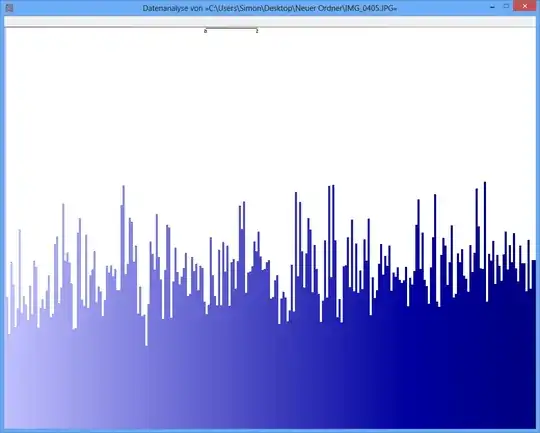
Example: The entropy of some JPG file is 7,9961532 Bits/Byte, the entropy of some TrueCrypt-container is 7,9998857. This means with the entropy test I cannot detect a difference between encrypted and compressed data. BUT: as u may see on the first picture, obviously the bytes of the JPG-file are not distributed uniformely (at least not as uniform as the bytes from the truecrypt-container).

Another test can be the frequency analysis. The distribution of each byte is measured and e.g. a chi-square test is performed to compare the distribution with a hypothetic distribution. as a result, I get a p-value. when i perform this test on JPG and TrueCrypt-data, the result is different.

The p-Value of the JPG file is 0, which means that the distribution from a statistical view is not uniform. The p-Value of the TrueCrypt-file is 0,95, which means that the distribution is almost perfectly uniform.

My question now: Can somebody tell me why the entropy test produces false positives like this? Is it the scale of the unit, in which the information content is expressed (bits per byte)? Is e.g. the p-value a much better "unit", because of a finer scale?

Thank you guys very much for any answer/ideas!

JPG-Image TrueCrypt-Container

Answer 1

This question still lacks essential information, but I think I can make some intelligent guesses:

• The entropy of a discrete distribution $\mathbb{p} = (p_0, p_1, \ldots, p_{255})$ is defined as

  $$H(\mathbb{p}) = -\sum_{i=0}^{255} p_i \log_2{p_i}.$$

• Because $-\log$ is a concave function, the entropy is maximized when all $p_i$ are equal. Since they determine a probability distribution (they sum to unity), this occurs when $p_i = 2^{-8}$ for each $i$, whence the maximum entropy is

  $$H_0 = -\sum_{i=0}^{255} 2^{-8} \log_2{(2^{-8})} = \sum_{i=0}^{255} 2^{-8}\times 8 = 8.$$

• The entropies of $7.9961532$ bits/byte (i.e., using binary logarithms) and $7.9998857$ are extremely close both to each other and to the theoretical limit of $H_0 = 8$.

  How close? Expanding $H(\mathbb{p})$ in a Taylor series around the maximum shows that the deviation between $H_0$ and any entropy $H(\mathbb{p})$ equals

  $$H_0 - H(\mathbb{p}) = \sum_i \frac{(p_i - 2^{-8})^2}{2 \cdot 2^{-8} \log(2)} + O(p_i - 2^{-8})^3.$$

  Using this formula we can deduce that an entropy of $7.9961532$, which is a discrepancy of $0.0038468$, is produced by a root-mean-square deviation of just $0.00002099$ between the $p_i$ and the perfectly uniform distribution of $2^{-8}$. This represents an average relative deviation of only $0.5$%. A similar calculation for an entropy of $7.9998857$ corresponds to an RMS deviation in $p_i$ of just 0.09%.

  (In a figure like the bottom one in the question, whose height spans about $1000$ pixels, if we assume the heights of the bars represent the $p_i$, then a $0.09$% RMS variation corresponds to changes of just one pixel above or below the mean height, and almost always less than three pixels. That's just what it looks like. A $0.5$% RMS, on the other hand, would be associated with variations of about $6$ pixels on average, but rarely exceeding $15$ pixels or so. That is not what the upper figure looks like, with its obvious variations of $100$ or more pixels. I am therefore guessing that these figures are not directly comparable to each other.)

In both cases these are small deviations, but one is more than five times smaller than the other. Now we have to make some guesses, because the question does not tell us how the entropies were used to determine uniformity, nor does it tell us how much data there are. If a true "entropy test" has been applied, then like any other statistical test it needs to account for chance variation. In this case, the observed frequencies (from which the entropies have been calculated) will tend to vary from the true underlying frequencies due to chance. These variations translate, via the formulas given above, into variations of the observed entropy from the true underlying entropy. Given sufficient data, we can detect whether the true entropy differs from the value of $8$ associated with a uniform distribution. All other things being equal, the amount of data needed to detect a mean discrepancy of just $0.09$% compared to a mean discrepancy of $0.5$% will be approximately $(0.5/0.09)^2$ times as much: in this case, that works out to be more than $33$ times as much.

Consequently, it's quite possible for there to be enough data to determine that an observed entropy of $7.996\ldots$ differs significantly from $8$ while an equivalent amount of data would be unable to distinguish $7.99988\ldots$ from $8$. (This situation, by the way, is called a false negative, not a "false positive," because it has failed to identify a lack of uniformity (which is considered a "negative" result).) Accordingly, I propose that (a) the entropies have indeed been computed correctly and (b) the amount of data adequately explains what has happened.

---

Incidentally, the figures seem to be either useless or misleading, because they lack appropriate labels. Although the bottom one appears to depict a near-uniform distribution (assuming the x-axis is discrete and corresponds to the $256$ possible byte values and the y-axis is proportional to observed frequency), the top one cannot possibly correspond to an entropy anywhere near $8$. I suspect the zero of the y-axis in the top figure has not been shown, so that discrepancies among the frequencies are exaggerated. (Tufte would say this figure has a large Lie Factor.)