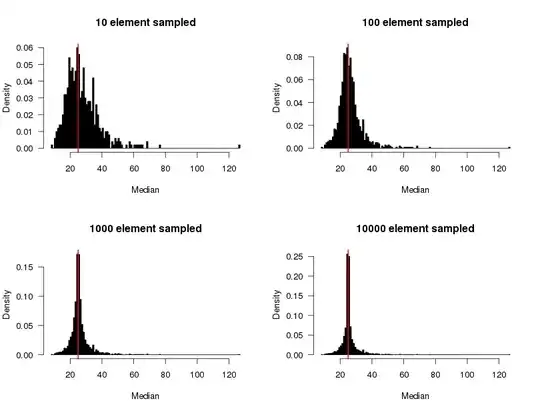
I'm working on a problem where I need to calculate the median for a very large data set (for instance, 100M values) that has a log-normal distribution. Because of the data set's size, we were thinking about taking a sample (say, a random subset of 2000 values), and calculating its median. While this is much nicer from a computation perspective, I am very worried it will be inaccurate.
What method could I use to determine how accurate this sampled median is?