7

In hypothesis testing, the definition of p value is the probability of obtaining test results at least as extreme as the results actually observed, under the assumption that the null hypothesis is correct.

Now, my understanding of what "extreme" means is based on @whuber's answer at What is the meaning of p values and t values in statistical tests?. They state that "more extreme" values refer to x values at which the likelihood ratio (the ratio of the likelihood under the null to the likelihood under the alternative) at x is greater than the likelihood ratio at the particular value observed for the test statistic.

For one sided hypothesis tests, this definition of "extreme" makes sense to me. However, I am still unsure how to find "more extreme" values when considering two sided tests. Let me use an example to illustrate.

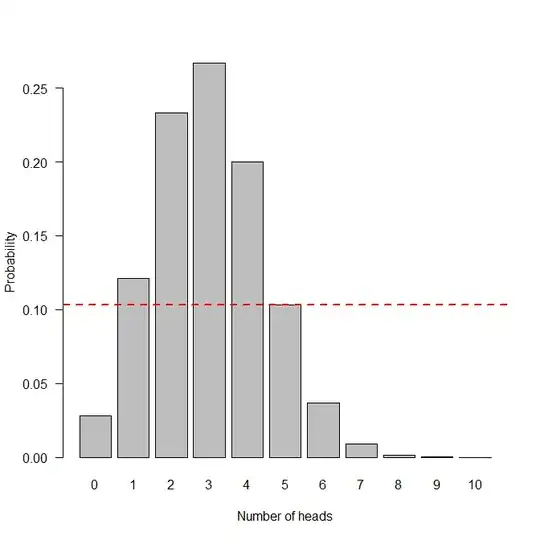
Suppose we are tossing a coin 10 times, and suppose the probability of getting a heads on any toss is p. Let $H_0: p=0.3$ and $H_1: p\ne 0.3$. Suppose that our test statistic is the total number of heads, which should follow a Binomial (10,0.3) distribution under the null hypothesis. Suppose that we observe 5 heads. I can see why when calculating the p value, we would need to include the probabilities of obtaining at least 5 heads, since the likelihood ratio at x=5,6,7,...,10 are all greater than or equal to the likelihood ratio at 5.

Now, I am told by those around me that x=0 and x=1 are also considered at least as extreme as x=5. So here's my question: why are the values x=0 and 1 considered as extreme as 5? I can't seem to use the likelihood ratio definition for "extreme values" to make sense of why 0 and 1 are considered as extreme as 5. Any help would be appreciated. If you don't want to use @whuber's definition of extreme, that's fine, but please do state your definition of extreme.

BruceET
  • 47,896
  • 2
  • 28
  • 76
  • 2
    Does this answer your question? [What is the meaning of p values and t values in statistical tests?](https://stats.stackexchange.com/questions/31/what-is-the-meaning-of-p-values-and-t-values-in-statistical-tests) – BruceET Sep 25 '20 at 20:28
  • 1
    One interpretation is that the mean under $H_0$ is $μ=np=10(.3)=3.$ So $X≥5$ and $X≤1$ are 'equally extreme' in terms of numbers of 'successes'. ("Two or more in either direction.") // However, I have just read @whuber's link and and recommend patiently reading all of it. – BruceET Sep 25 '20 at 20:32
  • Hi @BruceET, I don't think the link provided fully answers my confusion (in fact, I had already made a link to that particular link when I wrote the question). Actually, this question is in fact based on whuber's answer in the link provided. My original question was how you could use whuber's definition of extreme in order to make the conclusion that x<=1 are considered extreme values in the example I provided. –  Sep 25 '20 at 22:58
  • @BruceET, is your logic something that can be replicated no matter what the distribution of the test statistic is? As in, are you saying that extreme values are defined in general as being values that are at least as far from the mean (at least when testing two sided alternatives)? Because I don't see how this is consistent with the likelihood ratio definition, and would you be able to provide some source for this definition? –  Sep 25 '20 at 22:59
  • My intention is not to discredit anyone (so hopefully you don't take it that way) - it's just that I am looking for a formal / definitive way of determining extreme values in general (because I have seen so many inconsistencies in how extreme values are determined over the internet). I thought whuber's answer in the link originally mentioned would provide me with a general way of determining extreme values, but as my original question mentions, I do not see how I can use it to determine extreme values in the case of two sided hypothesis tests, such as in the example provided in the question. –  Sep 25 '20 at 22:59

1 Answers1

1

Here are the probabilities for $0, 1, \dots, 10$ heads if we throw a coin $n=10$ times under your null hypothesis of $p=0.3$:

probabilities

So let us assume that we have observed $n=5$ heads and wish to run a two-sided test. I have indicated the probability for observing $k=5$ under the null hypothesis of $p=0.3$ with the horizontal red dashed line. Take a look at the bars below that line.

What is an extreme outcome? It's an improbable one. Look at the probabilities. An outcome of $k=6$ is even more improbable than one of $k=5$, so it provides even more evidence against the null hypothesis. As do outcomes of $k=7, \dots, 10$. So these are all at least as improbable as the observed $k=5$, i.e., at least as extreme.

However, an outcome of $k=0$ would also be at least as improbable as $k=5$. If we had run the experiment twice with two different coins, and observed $k=5$ in one experiment and $k=0$ in the other, we would be more confident in rejecting the null hypothesis in the second than in the first.

In particular, when running the experiment only once (and testing two-sidedly), we need to include all events that are at least as improbable as the one we actually observed in calculating the $p$ value.

Note that this does not argue for including $k=1$ in our calculation, because it is (slightly) less improbable than the observed $k=5$. However, the difference in the probabilities under the null hypothesis is quite small, so one could reasonably argue that observing $k=1$ provides almost as much evidence against the null hypothesis as $k=5$, and so we should include it in calculating the $p$ value.

Stephan Kolassa
  • 95,027
  • 13
  • 197
  • 357
  • This argument is unconvincing for several reasons. The first is that the sense of "extreme" *must* depend on the null and alternative hypotheses, but this post's definition doesn't involve hypotheses. The second is that probabilities, to be sufficiently general, must concern *events* rather than outcomes--for continuous statistics all outcomes have zero probability--but then there is no total ordering of the probabilities of events. Even in this simple discrete case, the event $\{3\},$ say, is less probable than the event $\{0,1,5,6,7,8,9,10\},$ so by your lights it would be more "extreme"! – whuber Oct 08 '20 at 15:11