Interesting question. I have been active in both academic and applied forecasting for quite a while, and I can't recall anyone discussing CIs for MAPEs ever.
I don't think your calculation is very helpful. As an example, assume that the true holdout actuals are lognormally distributed with log-mean $\mu=1$ and log-SD $\sigma=1$. Assume further that our point forecast is a fixed $\hat{y}=\exp\big(\mu+\frac{\sigma^2}{2}\big)$ (which is an expectation forecast, which is not the MAPE-minimal forecast for lognormal data).
Recall the definition of a CI: it is an algorithm that, when the entire experiment is repeated often, will contain the true parameter value with a prespecified frequency. (Note that this is different from "there is a 95% chance that any one given CI contains the parameter.")
We can run our experiment by simulation. I get the true MAPE by simulating $n=10^6$ actuals, then repeatedly ($10^5$ times) draw the $n=4$ observations you have. In each case, I calculate APEs, take their mean and SD and calculate a 95% CI as you did. Finally, I record whether this simulated CI contained the true MAPE or not.
The hit rate is only 76%, instead of 95%.
R code:
set.seed(2020)
fcst <- exp(mm)
actuals <- rlnorm(1e6,meanlog=mm,sdlog=sqrt(ss.sq))
true_MAPE <- mean(abs(fcst-actuals)/actuals)
n_reps <- 1e5
hit <- rep(NA,n_reps)
n_obs <- 4
pb <- winProgressBar(max=n_reps)
for ( ii in 1:n_reps ) {
setWinProgressBar(pb,ii,paste(ii,"of",n_reps))
set.seed(ii) # for replicability
actuals <- rlnorm(n_obs,meanlog=mm,sdlog=sqrt(ss.sq))
APEs <- abs(fcst-actuals)/actuals
CI <- mean(APEs)+qt(c(.025,.975),n_obs-1)*sd(APEs)/sqrt(n_obs)
hit[ii] <- CI[1]<=true_MAPE & true_MAPE<=CI[2]
}
close(pb)
summary(hit)
Incidentally, we can change the experiment as follows: instead of a fixed point forecast, we can simulate $n=100$ iid "historical" observations, calculate the point forecast as their average (which, again, is an expectation forecast and not the MAPE-minimal one), then evaluate this point forecast on $n=4$ new observations, calculating a CI as above. The hit rate is pretty much unchanged.
You may find What are the shortcomings of the Mean Absolute Percentage Error (MAPE)? helpful.
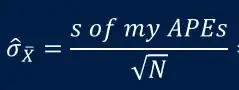 = A
= A