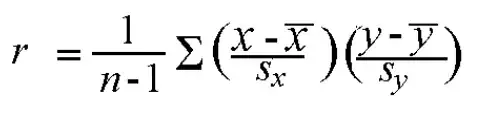Assume the two random variables $X$ and $Y$. The correlation of these two variables is given by the formula:
$\rho_{X,Y} = \frac{Cov(X,Y)}{\sigma_{X}\sigma_{Y}}$
Assume now that the two random variables become $\frac{1}{X}$ and $Y$. In this case the correlation becomes:
$\rho_{\frac{1}{X},Y} = \frac{Cov(\frac{1}{X},Y)}{\sigma_{\frac{1}{X}}\sigma_{Y}}$
My question is what is the relationship between $\rho_{X,Y}$ and $\rho_{\frac{1}{X},Y}$?
Does it hold that $\rho_{X,Y}= -\rho_{\frac{1}{X},Y}$? And if yes then what's the proof?