Mid-range via minimax

Question

_{Warning: crossposted at Mathematics SE.}

---

Given vector ${\rm a} \in \Bbb R^n$,

$$\begin{array}{ll} \displaystyle\arg\min_{x \in {\Bbb R}} & \left\| x {\Bbb 1}_n - {\rm a} \right\|_2^2\end{array} = \frac1n {\Bbb 1}_n^\top {\rm a} \tag{mean}$$

is the (arithmetic) mean of the entries of vector ${\rm a} \in \Bbb R^n$, whereas

$$\begin{array}{ll} \displaystyle\arg\min_{x \in {\Bbb R}} & \left\| x {\Bbb 1}_n - {\rm a} \right\|_1\end{array} \tag{median}$$

is a median of the entries of vector ${\rm a} \in \Bbb R^n$. Using the $\infty$-norm instead, what is the following?

$$\color{blue}{\boxed{\,\\\begin{array}{ll} \displaystyle\arg\min_{x \in {\Bbb R}} & \left\| x {\Bbb 1}_n - {\rm a} \right\|_{\infty}\end{array}}}$$

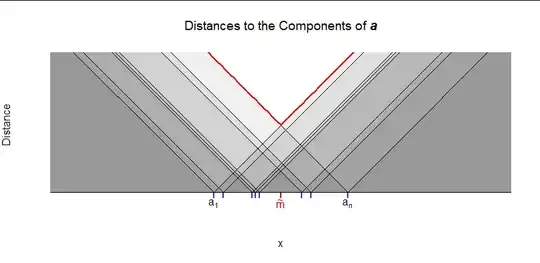
It appears to be the mid-range. I append a proof based on linear programming. Assuming that I have made no mistakes and my proof is indeed correct, I am interested in other proofs and in references.

---

My proof

$$\begin{array}{ll} \underset{x \in {\Bbb R}}{\text{minimize}} & \left\| x {\Bbb 1}_n - {\rm a} \right\|_{\infty}\end{array} $$

Introducing optimization variable $y \in {\Bbb R}$,

$$\begin{array}{ll} \underset{x, y \in {\Bbb R}}{\text{minimize}} & \qquad\qquad y\\ \text{subject to} & -y {\Bbb 1}_n \leq x {\Bbb 1}_n - {\rm a} \leq y {\Bbb 1}_n\end{array} $$

or, alternatively,

$$\begin{array}{lrl} \underset{x, y \in {\Bbb R}}{\text{minimize}} & y & \\ \text{subject to} & {\rm a} & \leq (x + y) {\Bbb 1}_n \\ & (x - y) {\Bbb 1}_n & \leq {\rm a}\end{array}$$

Let the entries of vector ${\rm a} \in \Bbb R^n$ be denoted by $a_1, a_2, \dots, a_n$. Note that there are many redundant inequalities:

• the set of $n$ inequalities ${\rm a} \leq (x + y) {\Bbb 1}_n$ can be replaced by $$x + y \geq \max \{ a_1, a_2, \dots, a_n \}$$

• the set of $n$ inequalities $(x - y) {\Bbb 1}_n \leq {\rm a}$ can be replaced by $$x - y \leq \min \{ a_1, a_2, \dots, a_n \}$$

Subtracting the latter inequality from the former inequality,

$$y \geq \frac{ \max \{ a_1, a_2, \dots, a_n \} - \min \{ a_1, a_2, \dots, a_n \} }{2} =: y_{\min}$$

and, thus,

$$ \begin{aligned} x &\geq \max \{ a_1, a_2, \dots, a_n \} - y_{\min} = \frac{ \min \{ a_1, a_2, \dots, a_n \} + \max \{ a_1, a_2, \dots, a_n \} }{2} \\\\ x &\leq \min \{ a_1, a_2, \dots, a_n \} + y_{\min} = \frac{ \min \{ a_1, a_2, \dots, a_n \} + \max \{ a_1, a_2, \dots, a_n \} }{2} \end{aligned} $$

Hence,

$$\begin{array}{ll} \displaystyle\arg\min_{x \in {\Bbb R}} & \left\| x {\Bbb 1}_n - {\rm a} \right\|_{\infty}\end{array} = \color{blue}{\frac{ \min \{ a_1, a_2, \dots, a_n \} + \max \{ a_1, a_2, \dots, a_n \} }{2}}$$

Some call this value the mid-range of $\{ a_1, a_2, \dots, a_n \}$.

Answer 1

1. Graphical demonstration

The components of vector $a$ are shown with blue ticks (a "rug plot"). $\tilde m$ is the midrange. It occurs at the lowest possible value of the upper envelope of the graphs of the distance functions $x\to |x-a_i|,$ shown in red.

2. Elementary demonstration using number properties

This demonstration essentially explains the graph rigorously: it points out that the upper red envelope consists of two sloping arms meeting at the midrange.

First let's set up some notation.

This objective function is the maximum distance between the number $x$ and the set of components of $a$ (a subset of the real numbers). Write $a_1$ for the least of those components and $a_n$ for the greatest. Let $\tilde m = (a_1+a_n)/2$ be their midrange, for which the maximum distance is $r = (a_n-a_1)/2.$

Here, then, is the demonstration:

If $x \lt \tilde m$ then $|x-a_n| \gt r$ and if $x \gt \tilde m$ then $x-a_1 \gt r.$ Consequently, the only possible candidate to minimize the objective function is $\tilde m$ itself, QED.