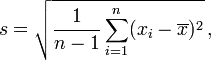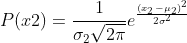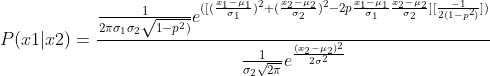I'm trying to derive the gaussian conditional distribution for a 2 variable gaussian. I'm doing this as I'm studying Gibbs and need to learn how to derive conditionals the analytic way; practice makes perfect.
The joint dist of x1 and x2:
The dist of x2:
I'm completely lost on simplifying the equation. I understand that the conditional of a normal is also a normal, but I'm not "seeing it" or even seeing how to move forward. My best guess is simplifying terms in the exponents. Buy in order to do so, I need to make the constant -1/2(1-P^2) go away in the joint. I'm not sure but I believe I can pull this out, as the natural log of this value.
If so, this would allow the terms to consolidate somewhat. Is this the right direction? Am I thinking about it wrong? (I am trying to solve this brute force analytically, not through a short cut which requires a proof of its own to understand.)
Edit: When I do as described above, factor the multiplied term out of the exponent, I end up with:
Not sure that this is beneficial. However, it does look slightly improved..