What is the best programmatic way for determining whether two variables are linearly or non-linearly or not even related

Question

What is the best programmatic way for determining whether two predictor variables are linearly or non-linearly or not even related, maybe using any of the packages scipy/statsmodels or anything else in python.

I know about the ways like plotting and manually checking. But I am looking for some other programmatic technique that is almost certain to differentiate whether a bivariate plot would be linear or non-linear or no relationship between them in nature.

I hear about the concept of KL divergence somewhere. Not really sure of the concept and in-depth, and whether can it really be applied for this sort of problem.

Answer 1

It is very difficult to achieve what you want programmatically because there are so many different forms of nonlinear associations. Even looking at correlation or regression coefficients will not really help. It is always good to refer back to Anscombe's quartet when thinking about problems like this:

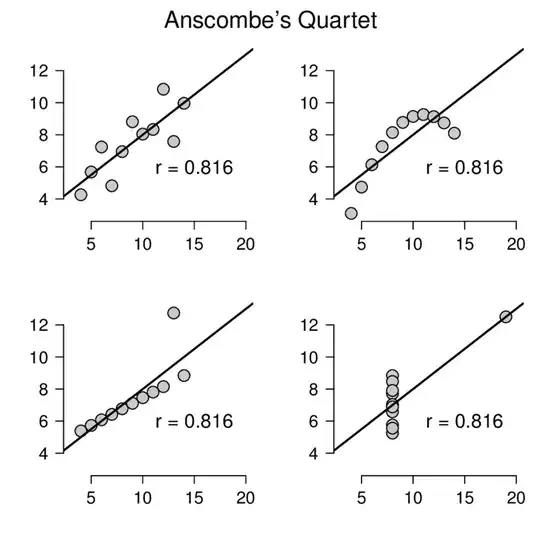
Obviously the association between the two variables is completely different in each plot, but each has exactly the same correlation coefficient.

If you know a priori what the possible non-linear relations could be, then you could fit a series of nonlinear models and compare the goodness of fit. But if you don't know what the possible non-linear relations could be, then I can't see how it can be done robustly without visually inspecting the data. Cubic splines could be one possibility but then it may not cope well with logarithmic, exponential and sinusoidal associations, and could be prone to overfitting. EDIT: After some further thought, another approach would be to fit a generalised additive model (GAM) which would provide good insight for many nonlinear associations, but probably not sinusoidal ones.

Truly, the best way to do what you want is visually. We can see instantly what the relations are in the plots above, but any programmatic approach such as regression is bound to have situations where it fails miserably.

So, my suggestion, if you really need to do this is to use a classifier based on the image of the bivariate plot.

1. create a dataset using randomly generated data for one variable, from a randomly chosen distribution.

2. Generate the other variable with a linear association (with random slope) and add some random noise. Then choose at random a nonlinear association and create a new set of values for the other variable. You may want to include purely random associations in this group.

3. Create two bivariate plots, one linear the other nonlinear from the data simulated in 1) and 2). Normalise the data first.

4. Repeat the above steps millions of times, or as many times as your time scale will allow

5. Create a classifier, train, test and validate it, to classify linear vs nonlinear images.

6. For your actual use case, if you have a different sample size to your simulated data then sample or re-sample to get obtain the same size. Normalise the data, create the image and apply the classifier to it.

I realise that this is probably not the kind of answer you want, but I cannot think of a robust way to do this with regression or other model-based approach.

EDIT: I hope no one is taking this too seriously. My point here is that, in a situation with bivariate data, we should always plot the data. Trying to do anything programatically, whether it is a GAM, cubic splines or a vast machine learning approach is basically allowing the analyst to not think, which is a very dangerous thing.

Please always plot your data.

Answer 2

Linear/nonlinear should not be a binary decision. No magic threshold exists for informing the analyst things like "definitely linear". It's all a matter of degree. Instead, consider quantifying the degree of linearity. This can be measured relative to explained variation in Y by two competing models: one that forces linearity and one that doesn't. For the one that doesn't a good general-purpose approach is to fit a restricted cubic spline function (aka natural spline) with say 4 knots (the number of join points, here the number of points at which the 3rd derivative is allowed to be discontinuous) needs to be a function of the sample size and expectations about the possible complexity of the relationship.

Once you have both linear and flexible fits you can use either log-likelihood or $R^2$ to quantify explained variation in Y. As discussed in the RMS you can compute an "adequacy index" by taking the ratio of model likelihood ratio $\chi^2$ statistics (smaller model divided by larger model). The closer this is to 1.0 the more adequate is a linear fit. Or you can take the corresponding ratio of $R^2$ to compute relative explained variation. This is identical to computing the ratio of the variances of predicted values. More about relative explained variation is here.

When you do not know beforehand that something is linear, we use such quantifications to inform us about the nature of the relationship but not to change the model. If using standard frequentist models, to get accurate p-values and confidence bands one must account for all the opportunities the model was given to fit the data. That means using the spline model for estimates, tests, and confidence bands. So you could say "allow the model to be nonlinear if you do not know beforehand it is linear". And most relationships are nonlinear.

Answer 3

The biggest problem you have here is that "non-linear relation" is not well defined. If you allow for any non-linear relation, there's basically no way to tell if something is "completely random" or just follows a non-linear relation that looks exactly like something that might come out of a "completely random" set up.

However, that doesn't mean you have no way to approach this problem, you just need to revise your question better. For example, you can use the standard Pearson's correlation to look for linear relations. If you want to look for monotonic relations, you can now try Spearman's Rho. If you want to look for potentially non-monotonic relations that still provide some ability to predict y given x, you can look at distance correlation. But note that as you get more flexible in what you call "correlated", you will have less power to detect such trends!

Answer 4

It's relatively simple to measure linearity. To distinguish between non-linear relationship and no relationship at all, you're basically asking for a chi-squared test with a number of boxes equal to the number of possible values. For continuous variables, that means if you do a full resolution test, you'll have only one data point per box, which obviously (or I hope it's obvious) doesn't yield meaningful results. If you have a finite number of values, and the number of data points is sufficiently large compared to the number of values, you can do a chi-squared test. This will, however, ignore the order of the boxes. If you want to privilege possible relationships that take into account order, you'll need a more sophisticated method. One method would be to take several different partitions of the boxes and run the chi-squared test on all of them.

Getting back to the continuous case, you again have the option of taking a chi-squared of a bunch of different partitions. You can also look at candidate relationships such as polynomial and exponential. One method would be to do a nonlinear transformation and then test for linearity. Keep in mind that this can cause results that you may find non-intuitive, such as that x versus log(y) can give a p-value for linearity that's different from exp(x) versus y.

Another thing to keep in mind when doing multiple hypothesis tests is that the $\alpha$ you choose is how much probability mass you have to distribute among all false positives. To be rigorous, you should decide beforehand how much you're going to distribute among all the hypotheses. For instance, if your $\alpha$ is $0.05$ and you have five alternative hypotheses you are testing, you can decide beforehand that you'll reject the null only if one of the alternatives have $p < 0.01$.