What model to choose for GLM - is my data really beta distributed?

Question

I have a question concerning GLMs.

I carried out a test to see how far changing different variables during data processing changes the OOB error of a Random Forest model. Three variables were varied (range in parentheses) called SNR (3-20), HWS (5-30) and Baseline (5-30). The dependent variable is the RF OOB error that can range from 0 to 1 and actually ranges from 0.12 to 0.26.

I wanted to carry out a GLM to see which independent variable influences the OOB error most. Here, I need to specify the distribution of the dependent variable. To do so, I used the command descdist in r (https://www.rdocumentation.org/packages/fitdistrplus/versions/1.1-1/topics/descdist) as was recommended here (How to determine which distribution fits my data best?). The resulting plot emphasizes that my data is beta distributed. I have read into GLMs a bit and found that GLMs cannot be done with beta distributed dependent variable. I have read that beta distribution can be neither 0 nor 1. In fact this would be possible with my dependent variable - but does this matter? Are the premises for a beta distribution violated by the potential of the dependent variable of being 0 or 1?

Another question: If my dependent variable is in fact beta distributed and GLMs cannot be built with it, what test can I carry out instead to find the most influential independent variable?

/edit: Here are some lines of data. In total it is more than 12.000 rows

Baseline iterations;Peak detection HWS;SNR;OOB-error
30;30;20;0.227060653
30;29;20;0.229393468
30;28;20;0.222395023
30;27;20;0.221617418
30;26;20;0.224727838
30;25;20;0.238724728
30;24;20;0.234059098
30;23;20;0.224727838
30;22;20;0.224727838
30;21;20;0.213063764
30;20;20;0.217729393
30;19;20;0.207620529
30;18;20;0.213063764
30;17;20;0.201399689
30;16;20;0.192846034
30;15;20;0.188180404
30;14;20;0.17962675
30;13;20;0.191290824
30;12;20;0.183514774
30;11;20;0.188958009
30;10;20;0.17962675
30;9;20;0.183514774
30;8;20;0.177293935
30;7;20;0.17651633
30;6;20;0.177293935
30;5;20;0.17651633
29;30;20;0.233281493
29;29;20;0.230171073
29;28;20;0.234836703
29;27;20;0.217729393
29;26;20;0.223950233
29;25;20;0.230171073
29;24;20;0.230948678
29;23;20;0.230948678
29;22;20;0.220839813
29;21;20;0.212286159
29;20;20;0.209953344
29;19;20;0.211508554
29;18;20;0.202177294
29;17;20;0.198289269
29;16;20;0.200622084
29;15;20;0.199066874
29;14;20;0.188958009
29;13;20;0.183514774
29;12;20;0.192068429
29;11;20;0.193623639
29;10;20;0.171073095
29;9;20;0.17962675
29;8;20;0.171073095
29;7;20;0.18118196
29;6;20;0.171073095
29;5;20;0.180404355
28;30;20;0.227060653
28;29;20;0.223950233
28;28;20;0.223950233
28;27;20;0.223950233
28;26;20;0.227838258
28;25;20;0.225505443
28;24;20;0.232503888
28;23;20;0.220062208
28;22;20;0.221617418
28;21;20;0.216951788
28;20;20;0.216174184
28;19;20;0.220062208
28;18;20;0.209953344
28;17;20;0.209953344
28;16;20;0.196734059
28;15;20;0.192846034
28;14;20;0.200622084
28;13;20;0.184292379
28;12;20;0.191290824
28;11;20;0.193623639
28;10;20;0.190513219
28;9;20;0.181959565
28;8;20;0.180404355
28;7;20;0.186625194
28;6;20;0.178849145
28;5;20;0.175738725
27;30;20;0.230948678
27;29;20;0.223950233
27;28;20;0.225505443
27;27;20;0.222395023
27;26;20;0.222395023
27;25;20;0.226283048
27;24;20;0.228615863
27;23;20;0.227838258
27;22;20;0.223172628
27;21;20;0.212286159
27;20;20;0.216174184
27;19;20;0.202177294
27;18;20;0.199844479
27;17;20;0.210730949
27;16;20;0.201399689
27;15;20;0.200622084
27;14;20;0.190513219
27;13;20;0.195178849
27;12;20;0.193623639
27;11;20;0.192068429
27;10;20;0.188180404
27;9;20;0.17962675
27;8;20;0.175738725
27;7;20;0.185069984
27;6;20;0.178849145
27;5;20;0.17496112

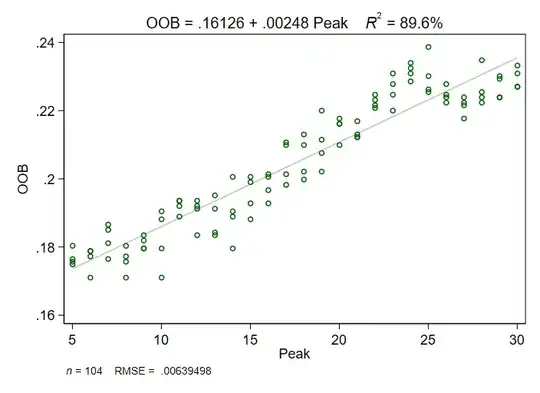
/edit2: I added an image showing the relation of the indpendent variables to the DV

What's most important here is functional relationship and so choosing a link. In your case mean OOB error is clearly bounded between 0 and 1 and so a logit link is suggested. In practice, other links may work as well or better, even identity links. The Cullen and Frey graph can be helpful but it's far from indicating unequivocally what kind of distribution you have. I wouldn't worry much about whether you really have a beta distribution. Can you post (example) data? A random sample of 100 or so would be enough to give flavour and if your dataset is smaller then by all means list them all. — Nick Cox, Sep 07 '20 at 08:11
https://stats.stackexchange.com/questions/189190/glm-with-logit-link-and-gaussian-family-to-predict-a-continuous-dv-between-0-and points in helpful directions. — Nick Cox, Sep 07 '20 at 08:20
Dear Nick. Thank you for your comments. So if the link is most important I can chose a distribution family that is at least similar to what I expect from my data? I added some line of data in the starting post and will read into the suggested link. — S.R., Sep 07 '20 at 09:22

Nick Cox · Accepted Answer · 2020-09-07T09:28:48.257

Thanks for the data example. SNR is constant in your sample, so the data example doesn't allow any assessment of its role or importance. I tried (1) a plain regression and (2) a GLM with logit link, binomial family and robust standard errors with almost identical indications. Peak is much more important than Baseline.

However, this scatter plot suggests to me a S-shaped relationship between OOB and Peak. Is there any substance to that? (RMSE does indeed have too many decimal places.)

You have a bounded response or outcome (you say "dependent variable") and in principle respecting those bounds is important, but in practice they won't bite here. There are plenty of examples in statistics of data not matching assumptions exactly, but closely enough that they don't bite. For example, a Gaussian or normal is in principle unbounded and can (will) be negative as well as positive, but that doesn't stop it being a good approximation to people's heights. Other way round, your response looks much shorter-tailed in its marginal distribution than a Gaussian, but the data themselves don't hint at 0 and 1 as bounds.

I added some graphs to the original post showing the relations of all variables to the DV. To me it seems you are correct converning the S-shaped relation of Peaks and OOB. So it needs some kind of further curve fitting? — S.R., Sep 07 '20 at 09:48
I would use a more empirically-based model such as a generalized additive model. Although the S pattern looks genuine the scatter is too much to support e.g. a logistic-type curve with minimum and maximum and from what you say there aren't arguments in principle for firm bounds other than 0 and 1 and the other predictors have some role too. — Nick Cox, Sep 07 '20 at 11:45

What model to choose for GLM - is my data really beta distributed?

1 Answers1