Multiplying vectors by the covariance matrix?

Question

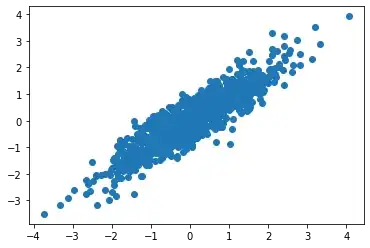
I thought I knew covariance but I'm starting to think that there's more to it. For example, what happens when you multiply observations by their corresponding covariance matrix? [x1,y1] * cov(x,y). I did a little experiment and am interested by the outcome.

import matplotlib.pyplot as plt
import numpy as np

mean = [0, 0]
cov = [[1, 0.9], [0.9, 1]] 

x, y = np.random.multivariate_normal(mean, cov, 1000).transpose()
plt.scatter(x, y)
plt.show()

new_x = []
new_y = []
for i in range(500):
  vec = np.array([x[i],y[i]])
  trsf = np.matmul(vec.transpose(),cov)
  new_x.append(trsf[0])
  new_y.append(trsf[1])

plt.scatter(new_x,new_y)

As you can see, every (x,y) pair is projected onto a line w/o any deviation. I'm curious what's actually happening? My guesses are (A) these data points are projected onto the OLS line. Or (B) these data point are projected onto the leading eigenvector of the covariance matrix.

Any thoughts/ideas?

This multiplication is rare. After all, consider its units of measurement: they are in squared (x) times squared (y). The *meaningful* operations include multiplying the vector by the *inverse* of the covariance matrix: that will be unitless, already suggesting it may have (and does have) a universal meaning. — whuber, Sep 06 '20 at 21:43
@whuber I see inverse of covariance matrix come up at times (and the determinant, too) as you alluded, what does this mean? — jbuddy_13, Sep 06 '20 at 21:47
That could be interpreted in many ways. One interesting setting is described at https://stats.stackexchange.com/questions/62092, where you will see the inverse appear prominently in the calculation of the Mahalanobis distance. — whuber, Sep 07 '20 at 18:49

gunes · Accepted Answer · 2020-09-06T20:54:17.417

They're not exactly on a line, but yes, they generally follow the main eigenvector because the projected point has the following coordinates (assuming $x$ with dimensions $2\times 1$):$$\Sigma x=\sigma_1u_1u_1^Tx+\sigma_2u_2u_2^Tx=(\sigma_1<u_1,x>)u_1+(\sigma_2<u_2,x>)u_2$$ Here, $u_i$ are eigenvectors, and $\sigma_i$ are eigenvalues. Since $\sigma_1>\sigma_2$ and for the most of the data component in the direction of $x_1$ is larger than the one in $x_2$, the coefficient before $u_1^T$ is typically much larger than the one before $u_2^T$. This causes the points align with the first eigenvector mostly.

If there were some outliers, especially nearly perpendicular to the first eigenvector, they would not be aligned so much with $u_1$'s direction.

import matplotlib.pyplot as plt
import numpy as np

mean = [0, 0]
cov = [[1, 0.9], [0.9, 1]] 

x, y = np.random.multivariate_normal(mean, cov, 1000).transpose()
x = np.hstack([x, -10])
y = np.hstack([y, 10])

plt.scatter(x, y)
plt.show()

new_x = []
new_y = []
for i in range(len(x)):
  vec = np.array([x[i],y[i]])
  trsf = np.matmul(vec.transpose(),cov)
  new_x.append(trsf[0])
  new_y.append(trsf[1])

plt.scatter(new_x,new_y)

I haven't seen so far. This is basically about what happens with the data. — gunes, Sep 06 '20 at 21:19
$\Sigma x$ taken a step further: what can be said about the meaning of $x' \Sigma x$? — develarist, Sep 07 '20 at 01:45
@develarist, I'm not sure that anything can be said. However, `[x.T] inverse(sigma) [x]` is super common. I believe that means x scaled by the amount of information on the vector x. But I'm not sure...? — jbuddy_13, Sep 07 '20 at 15:52

Multiplying vectors by the covariance matrix?

1 Answers1