Hessian optimization (Newton method) using the direction given by the gradient to make the next iteration step of the parameters

Question

Reading Deep Learning Book (page 86) I am having trouble understanding the reasons behind using the gradient ($g$) as the direction of the step of the parameters ($x$).

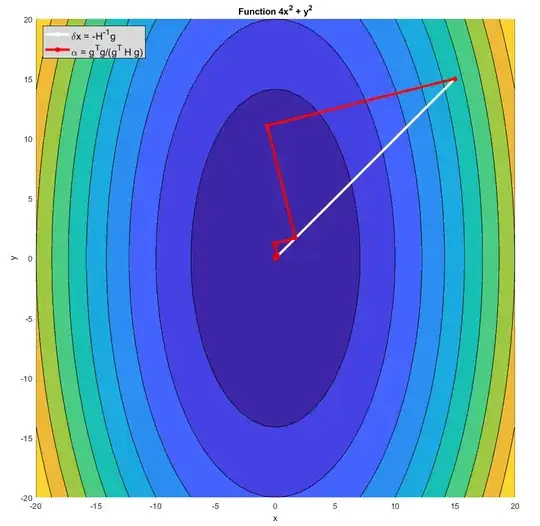
I understand that the Newton method consists on minimizing the second-order Taylor series approximation of the function ($f(x_o + \delta x)$) given by: $$ f(x_o + \delta x) \approx f(x_o) + \delta x^T g +\frac{1}{2}\delta x^T \,H \,\,\delta x$$ Where $g$ is the gradient and $H$ is the hessian matrix. Thereby minimizing this expression w.r.t. $\delta x$ we obtain that the step direction should be $\delta x= -H^{-1}\,g$, so this is a direction different from the gradient.

But in the approach given in the text book, this step direction is given by a direction proportional to the gradient: $\rightarrow \delta x = \alpha \,g$ where $\alpha$ is the learning rate (scalar). Thereby minimizing $f(x_o + \delta x)$ with respect to $\alpha$ we can obtain that this learning rate should be the right term:

$$ f(x_o + \delta x) \approx f(x_o)+ \alpha g^T g + \frac{1}{2} \alpha^2 g^T H g \,\,\,\,\,\,\,\,\,\,\rightarrow \,\,\,\,\,\,\,\,\,\,\alpha = \frac{g^Tg}{g^THg}$$

What I am having difficulties with is understanding if with this second approach we are able to make use of the curvature of the function, $f(x)$, in order to make the next step on the parameters ($x$). So my questions are:

1. Considering $\delta x = \alpha g$, are we able to take account of the curvature of the function in order to make the next iteration of $x$?
2. Which are the advantages of using $\delta x = \alpha g$ in comparison to $\delta x= -H^{-1}\,g$?

Thanks in advance.

Answer 1

My bad, a few pages later the author explains that the second approach (using $\delta x = \alpha g$ with $\alpha = g^Tg/(g^THg$)) does not take account of the curvature.

In case it may help to someone and in order to visualize this, I have plotted the optimization paths for each method for the function $4x^2 + y^2$ and starting point $(15,15)$:

As expected we can see there that only the step made by the original Newton method ($\delta x = -H^{-1}g$) takes advantage of the curvature of the function.