I am trying to prove that 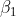 equals
equals 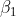 in the following two equations given that the vector
in the following two equations given that the vector 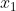 are the same in both:
are the same in both:
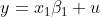

The only two assumptions for both equations given are the homoskedastic assumption (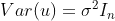 ) and the orthogonality of the vectors
) and the orthogonality of the vectors 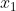 and
and 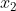
Any help would be greatly appreciated, thank you