6

Say we know that $Y$ follows a distribution with density $f$. It is well known that the mean $E(Y \ | X)$ minimizes the Root Mean Square Error (RMSE). We are generally interested in predicting a value for $y $ given we know $x$ as $E(Y \ | \ X)$.

Then, even if theoretically we might want to model $f$, if we just want a deterministic prediction, Why even bother with different distributional assumptions on $Y \ | \ X$, i.e. why even bother with different cost functions like the negative log-likelihood?

Examples:

  • Suppose $Y \sim Bernoulli(p)$. If we use RMSE as cost function this clearly minimizes the mean of $Y$, which is indeed $p$, the value we want.
  • Suppose $Y \sim Gamma(k, \theta)$. Since $E(Y) = k\theta$, we can just fix e.g. $\theta = 1$ and predict as $E(Y) = k$. Again, let us use RMSE as cost function and this will obtain the intended value. So, Why use for example the negative log likelihood of the gamma distribution?
D1X
  • 733
  • 1
  • 5
  • 21
  • 1
    because $E(y|x)$ is only theoretically true. we might be lucky to get the estimates right *in-sample*, but often have to resort to cost functions that provide a solution that also holds up *out-of-sample* – develarist Sep 02 '20 at 09:53
  • just because it's true in expectation doesn't mean it will be true in your realisation. If I gave you one method which gives you the correct answer in expectation but with a variance of 100, or another method which is biased and gives you (correct answer+1) in expectation but with a variance of 10, you would probably choose the latter – gazza89 Sep 02 '20 at 10:50
  • your examples with Bernoulli and gamma distributions can only go so far when real data in many fields often do not conform to any pre-specified density – develarist Sep 02 '20 at 13:26
  • @develarist Could you elaborate on that answer? Of course real data often does not conform to any specific distribution, but an assumption over the distribution is always made. I made the question under a theoretical framework and added some examples simply to make it a little less *arid* – D1X Sep 02 '20 at 14:25
  • the examples were good since many would probably have responded with $E(Y|X)$ for the Gaussian case which requires linearity, but assumptions of density within models are often the reason why models themselves don't perform well empirically. There's no reason to believe "expectations" are "certain". Machine learning tries to reduce uncertainty in model output by offering a variety of cost functions to choose from – develarist Sep 02 '20 at 14:28
  • *"if we just want a deterministic prediction"* What do you mean by a deterministic prediction? – Sextus Empiricus Oct 15 '20 at 16:23
  • @SextusEmpiricus I mean we want to predict a single value, as opposed to e.g. using the distribution of $y|x$ to generate samples. – D1X Oct 16 '20 at 08:39
  • @D1X so you do recognize that the prediction of the single value will not be deterministic but instead is subject to random variation? (and we might wish to optimize our prediction procedure in order to optimize the expected value of some cost function, e.g. minimize the squared error of the prediction) – Sextus Empiricus Oct 16 '20 at 08:49
  • @SextusEmpiricus Yes it will be subject to randomness coming from the sample, machine learning algorithm and so on... What I mean is, for the sake of this question we are interested in obtaining a point estimate of $E(y | x)$. – D1X Oct 16 '20 at 08:59
  • @D1X but don't you want the point estimate that is best according to some measure. If you don't care about the performance according to some measure (cost function) then you can just as well use $\mu_y=42$ as point estimate. – Sextus Empiricus Oct 16 '20 at 09:32
  • @SextusEmpiricus Mhm... I don't get what you mean – D1X Oct 16 '20 at 09:50
  • @D1X nice pun. You ask "why bother with cost functions?" and seem to argue that we should not need to be bothered with it "I already have the sample mean, or least squares estimate, which works fine for me, so I should not need a cost function?". But *how* do you determine what is 'fine'? How do you determine when one estimate is better than another? For this you need a cost function – Sextus Empiricus Oct 16 '20 at 09:54
  • Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/115161/discussion-between-d1x-and-sextus-empiricus). – D1X Oct 16 '20 at 09:55

3 Answers3

8

The mean minimizing the root mean square error is often not the practical situation

It is well known that the mean E(Y |X) minimizes the Root Mean Square Error (RMSE).

You are right, the theoretical mean $E(Y |X) $ minimizes the root mean square error of a prediction (independent of the distribution). So if minimizing the mean square error of a prediction is your goal and you know the theoretical mean, then indeed you do not need to care about the distribution (except whether the mean and variance exist for the distribution).

However, often this theoretical mean is unknown and we use an estimate instead. Or we want to minimize something else than the mean squared error. In those cases you often need to use assumptions about the distribution of the errors in order to determine which estimator to use (to determine which one is optimal).

So a typical situation is

  • gathering data from a population
  • compute an estimate of the distribution of the population based on the data
  • use the estimates directly (e.g. make some decision based on the estimates)
  • or use the estimates to make a prediction (in which case the error due to the randomness in the population get's on top of the randomness of the estimates about this population)

The situation that you sketch makes a shortcut to the final point and assumes that we know the population. This is very often not the case. (It can still be a practical case, for instance if we have so much information, a large sample, such that we can estimate the population distribution with high accuracy and the biggest error in the prediction is due to the randomness in the population)

If the predicted value of machine learning method is $E(y | x)$, why bother with different cost functions for $ y | x$?

A machine learning method does not provide $E(y|x)$ it provides an estimate of $E(y|x)$. How good or bad estimators and predictors are will depend on the underlying distribution of the population (from which we can deduce the sample distribution of our estimator and predictor).

Example: Say we wish to estimate the location parameter of a Laplace distributed population (and use that for prediction). In that case the sample median is a better estimator than the sample mean (ie. The distribution of the sample median will be closer to the true parameter than the distribution of the sample mean. The error of the estimate will be smaller).

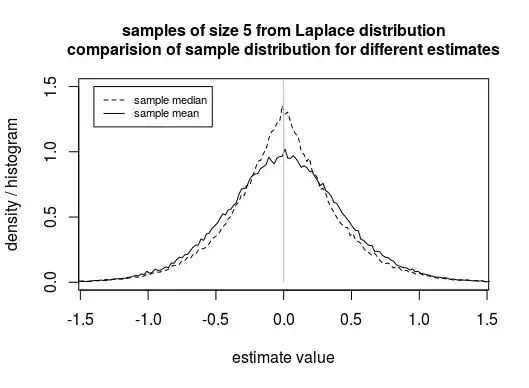
showcase that median can be better than mean

Image: showcase that the sample median can be a better estimator than the sample mean. Note that the distribution is more concentrated around the true location parameter (in this example this is 0).

So based on the assumption that the errors are Laplace distributed we should decide to use the sample median as an estimator and predictor, and not the sample mean.

Difference between cost function used for fitting and cost function used for evaluation.

Another underlying issue is about the differences in cost functions.

The cost function that is used to perform the fitting can be different from the cost function that is the objective.

In the previous example with the Laplace distribution, the objective might be to minimize the expected mean squared error of the estimate/prediction. But, we find the estimate that optimizes this objective by minimising the mean absolute error of the residuals.

A related question is: Could a mismatch between loss functions used for fitting vs. tuning parameter selection be justified? In that question you minimize the (objective) cost function by cross validation, but in the answer it is demonstrated that it is still good to perform the fitting (during training) by means of a cost function that relates to the distribution of the error of the measurements.

quote from the chat

"My question had to do with how to choose one estimator or another one (i.e. one loss function over another one)"

An estimator can be expressed as the argmin of some cost function of the data/sample (e.g. the sample mean minimizes the sum of squared residuals, and the sample median minimizes the sum of absolute residuals).

However, that is a different cost function than the cost function used to describe the performance of an estimator.

So that's why we are bothered with cost functions. Those cost functions allow us to evaluate the performance of an estimator. We can compute/estimate how often an estimator X make a particular error and compare it with how often an estimator Y makes that particular error. And since there are many sizes of errors we make a weighted sum of all possibilities by some cost function.

E.g. the distribution of errors for estimator X and Y might be (a simplistic example)

Error size.                  -2     -1     0      1     2     
frequency for estimator X   0.00   0.25   0.50  0.25   0.00
frequency for estimator Y   0.02   0.18   0.60  0.18   0.02

The estimator X has a higher mean absolute error (half the time the error is $\pm1$ and the mean absolut error is 0.5. For the estimator Y it is 0.44).

However in terms of the expected mean squared error the estimator X (with 0.5) is lower than the estimator Y (with expected mean squared error 0.52).

To compute these comparisons you need to be able to know/estimate the sample distribution of the estimators (like in the above example this is done for the Laplace distribution and the sample mean and the sample median) and some cost function to compare those distributions.

(In the case of the Laplace distribution and the sample mean vs sample median, you have that the sample median is stochastically dominant and for any convex cost function the sample median will be better than the sample mean, so you do not always need to know the evaluation cost function in detail. Related question: Estimator that is optimal under all sensible loss (evaluation) functions)

R-code to create the graph

### generate data
set.seed(1)
s <- 100000
n <- 5
x <- matrix(L1pack::rlaplace(s*n,0,1),s)
medians <- apply(x,1,median)
means <- apply(x,1,mean)

### compute frequency histogram
breaks <- seq(floor(min(medians,means)),ceiling(max(medians,means)), 0.02)
hmedians <- hist(medians, breaks = breaks)
hmeans <- hist(means, breaks = breaks)

### plot results
plot(hmedians$mids, hmedians$density, type = "l",
     ylim=c(0,1.5), xlim = c(-1.4,1.4),
     xlab = "estimate value", ylab = "density / histogram",
     lty=2)

lines(hmeans$mids, hmeans$density)
lines(c(0,0),c(0,2),lty=1,col="gray")
title("samples of size 5 from Laplace distribution
comparision of sample distribution for different estimates", cex.main = 1)

legend(-1.4,1.5, c("sample median","sample mean"), lty = c(2,1), cex = 0.7)
Sextus Empiricus
  • 43,080
  • 1
  • 72
  • 161
  • For your particular example: Why is the sample median a *better* estimator than the mean. The sample mean is an unbiased estimator of the population mean, which coincides with the location parameter. – D1X Oct 16 '20 at 08:50
  • @D1X I will add a graph of their sample distributions – Sextus Empiricus Oct 16 '20 at 08:51
  • @D1X your question made me confused about your use of E(Y|X). I guess that with this you mean the *theoretical* conditional mean and not the *estimate*. I had assumed the latter because you call E(Y|X) the output of a machine learning method (and the output is an estimate). I have edited my question now. – Sextus Empiricus Oct 21 '20 at 11:09
3

Say we know that Y follows a distribution with density f.

If that statement is true, you would not want to try different distributional assumptions. If it is not true, then you should consider modeling different assumptions because it can have a substantial impact on your results.

why even bother with different cost functions like the negative log-likelihood?

Because we should be using our true loss function. Unfortunately, the training most people get doesn't really give them a way to really parse through the issues with varying the loss function.

Let me give you a real-world problem. Some things must be purchases such that $x\ge{k}$ where $k$ is an unknown constant. If $x<k$ then one hundred percent of the material purchased is unusable and must be destroyed. You must then begin again.

If you purchase $x>k$ then $x-k$ must be destroyed and is a loss.

On either side, the loss per unit is the waste times $c$.

Suppose $k=1000$ and $\hat{k}=999$, while $c=\$1000$. Being one unit to the left will cost you \$999,000. One unit to the right will cost you \$1,000.

Minimizing quadratic loss would imply you should take catastrophic losses fifty percent of the time. The expectation is a disaster.

Solutions to real world problems can be markedly suboptimal if you use the RMSE as your objective function.

Dave Harris
  • 6,957
  • 13
  • 21
  • *Minimizing quadratic loss would imply you should take catastrophic losses fifty percent of the time.* I guess this would be correct if we were talking about the median but not the mean? – Richard Hardy Apr 05 '21 at 04:22
3

The answer is simpler than it seems. Though the sample mean in the simplest case, or least squares estimates in the multivariable predictor case provide unbiased estimates of the long-run mean, these estimates can be wrong or highly inefficient. In the case of a simple mean, i.e., when there are no predictors X, if the sample comes from a log-normal distribution the sample mean on the original scale is a terrible estimate of E(Y). The best estimator is a function of the mean and standard deviation after taking logs. In the multivariable situation, a least squares estimate of E(Y|X) provides unbiased estimates of the mean if the model structure is correctly specified for the right hand side of the model, but the estimates of E(Y|X) as a function of X can be wrong for every observation in the sense that all the regression coefficients are wrong even though they "add up" to something that is right. If Y|X has a lognormal distribution, for example, and you did not take log(Y) when computing least squares estimates, you will get bad predictions when you examine the predictions in an X-specific manner.

Frank Harrell
  • 74,029
  • 5
  • 148
  • 322