0

I read an article that explained why high values of R-squared values do not always indicate a good model .

But I have trouble understanding their justification .

Here is what I read :

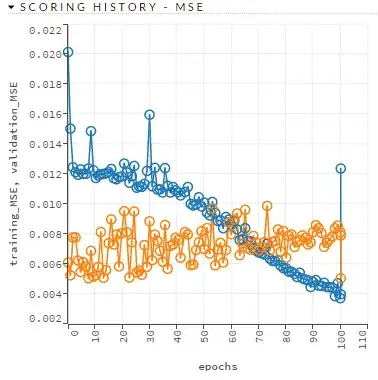
" No! A high R-squared does not necessarily indicate that the model has a good fit. That might be a surprise, but look at the fitted line plot and residual plot below. The fitted line plot displays the relationship between semiconductor electron mobility and the natural log of the density for real experimental data.

enter image description here

enter image description here

The fitted line plot shows that these data follow a nice tight function and the R-squared is 98.5%, which sounds great. However, look closer to see how the regression line systematically over and under-predicts the data (bias) at different points along the curve. You can also see patterns in the Residuals versus Fits plot, rather than the randomness that you want to see. This indicates a bad fit, and serves as a reminder as to why you should always check the residual plots. "

What I don't understand about this explanation is , "the regression line systematically over and under-predicts the data (bias) at different points along the curve" . To me , the curve seems pretty good and has fit well to the data . It also has a high R-squared value , then why do they say this is a bad fit ?

Can someone please elaborate on this ? I am having trouble understanding their explanation and also why high R-squared values need not always indicate a good model .

Bharathi
  • 147
  • 1
  • 9
  • 1
    Your blue line suggests that, for high density, mobility tends to decrease as density increases. Your data dots do not suggest that. So the fitted model may be seriously misleading. More generally, the pattern of the residuals suggest systematic problems with the model since you can reasonably predict that when interpolating it will usually overestimate mobility in some obvious parts and in other parts underestimate mobility; this issue may suggest that it is not a good model. – Henry Aug 28 '20 at 17:25
  • Have you seen https://stats.stackexchange.com/questions/13314? – whuber Aug 28 '20 at 18:28

1 Answers1

0

If a model is a good fit for the data, then you will see uniformly distributed points on the residual plot (2d picture). However, if you see a pattern, like on the second picture from the question, you may suggest a systematic bias at different points on the curve.

$R^2$ is often misleading for nonlinear models.
https://link.springer.com/content/pdf/10.3758/BF03329960.pdf

user1635327
  • 101