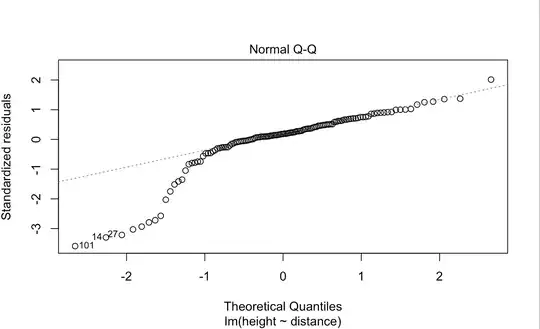
We know KL-divergence is sometimes expressed like this:
which shows it's capturing the deviation between the joint distribution of X and Y, and the product of marginals for X and Y. This suggests KL-divergence is simply the multiplication rule for independent events, reformulated in terms of entropy. In other words, if the joint fails to align with the product of marginals then it's expected the variables have some dependence structure.
We also see KL-divergence expressed like this:
How does this second expression relate to the first? I cannot see where the joint is being calculated, or the product of marginals for that matter.