4

Extensive edit of the original question while I've been able to refine my thoughts and write some better code.

Consider data from two processes, each with can produce many, many time series curves that will have lots of overlap in their results. An example image is below, using relatively few curves - the actual application has many thousands for each process whereas this only has 250 each (Red vs. Blue):

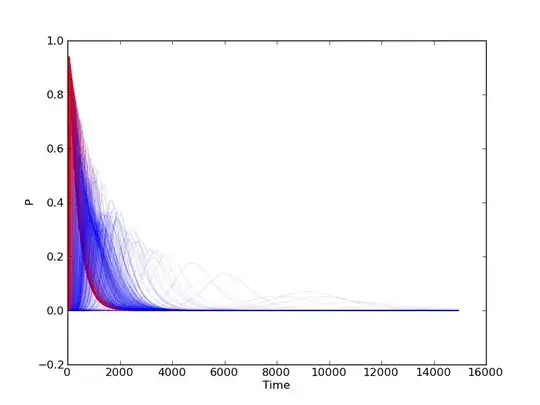
enter image description here

There will be a large amount of overlap between the two, but for example the "Red" process is the only one that can produce very high, very sharp peaks early on, whereas "Blue" seems to produce higher peaks in the X = 3000 to 4000ish range, etc. What I'm looking for is a way to statistically quantify or visualize that non-overlapping space where there's lots of overlap.

Anyone have any ideas? One thing I've considered doing is ignoring that these are time-series, and generating something like a kernel density for each and subtracting one from the other - areas far from zero would then be places of less overlap, but I'm not sure how defensible that is.

The actual application of this is a series of parameter searches for a dynamical system - essentially, the intent is to produce many, many numerical results of a system of differential equations using two different approaches, and then find anywhere in the results where, for example "Red can generate results with this value, whereas Blue cannot" when for the most part some parameter value for Red will provide the same results as a different parameter for Blue.

Fomite
  • 21,264
  • 10
  • 78
  • 137
  • It would help to provide a precise, quantitative definition of what you mean by "overlap." (I can think of *many* different interpretations in your time series context.) – whuber Jan 23 '13 at 18:24
  • The difference between the two distributions is indistinguishable because the variance of the series swamps any visible difference in the central tendency. A solution then is to approximate the plot the approximated distribution in the chart (most likley via some running, smooth estimate of the series). Examples can be found at [Preferred methods for graphing time-series data to present “averages”?](http://stats.stackexchange.com/a/11229/1036) and [Show series of exponential decay distributions in one chart](http://stats.stackexchange.com/a/18826/1036). – Andy W Jan 23 '13 at 18:58
  • This advice seems general enough to extend to however you want to characterize "overlap" - but some specific aesthetic qualities to display overlapping bands is to use strongly diverging colors and transparency judiciously (and only have a max of two groups in any one plot). – Andy W Jan 23 '13 at 19:00
  • @whuber See the edit, if that helps at all? – Fomite Jan 23 '13 at 19:15

1 Answers1

2

If by quantifying the overlap you're simply looking to quantify how much red area is away from the blue area, you could treat your two time series and calculate the Manhattan distance between them. This is essentially the sum of the absolute value of the differences between each point. (You may also be interested in other distances, perhaps the Chebyshev distance, which will certainly be interesting if you want to measure the peak differences.)

The example you're giving is jumping quite a lot (it looks like perfect noise). It's not clear whether actual experimental data would present such variations. It may be interesting to consider applying a moving average transformation first, although this will have a significant impact on the distances results.

If the phenomena are somewhat meant to be repeating themselves, it might be worth considering using signal processing techniques. In particular, you could compute an FFT on both time series and compare their resulting spectra. For example, comparing the first "bin" (the "DC component") should indicate how centered they are with each other. Using distances comparisons between each spectrum should also be an interesting comparison tool, possibly more relevant than doing this in the time domain. How to interpret this will certainly depend on the actual nature of the problem.

Bruno
  • 287
  • 1
  • 3
  • 9