Is 95% specific to the confidence interval in any way?

Question

I am aware of the misconception that a "95% confidence interval means there is a 95% chance that the true parameter falls in this range," and that the correct interpretation is that if you build, say, 100, of these confidence intervals from random sampling, then 95 of the confidence intervals should include the true parameter.

In https://www.econometrics-with-r.org/5-2-cifrc.html, I see the following:

Is this wording incorrect? It seems to be saying that the true value has a 95% chance of being in that specific confidence interval.

My second question is, say you have one of these 95 confidence intervals. Aside from using 95% to get the 1.96 Z-score, how else is the 95% manifested in this confidence interval?

@Stefan It sounds like it's saying the confidence interval has a 95% chance of containing the true value to me, but I'm not sure if I read it correctly. A bit new to the confidence interval and hypothesis testing realm. — user5965026, Aug 16 '20 at 05:31
@SextusEmpiricus I think I know what the OP meant with Q2 and added this bit to my answer. But I agree that the 2nd question is not 100% clear. — Stefan, Aug 16 '20 at 15:45
Isn't that the *definition* of having a 95% chance of X? That if you take the same scenario 95 times, X will happen in 95 of them? — user253751, Aug 17 '20 at 10:01
@user253751 When you flip a trick coin that lands heads with a probability of 95%, do you get 95 heads and 5 tails exactly every time? Maybe but probably not. However, if you were to flip that coin a very large number of times, the probability will eventually converge to 0.95 of flipping heads. So, **on average** you would expect 95 heads out of 100 flips. — Stefan, Aug 17 '20 at 15:22
@Stefan Do I need to say "about 95"? I think everyone understood what I meant. — user253751, Aug 17 '20 at 15:36
@user253751 well that's up to you how clear you want to make it to the reader, but judging by the vast amount of papers on the misinterpretation of confidence intervals, p-values, type I error rates, etc., it doesn't hurt to highlight that probability statements in frequentist statistics are the result of what one would expect if experiments were repeated a very large number of times and under the exact same conditions. — Stefan, Aug 17 '20 at 16:01
Now I see the confusion: "95% confidence interval" does not mean that if you measure the *population mean* 100 times, it will be within the confidence interval in about 95 of them. Does anyone think that? — user253751, Aug 17 '20 at 16:17
@user253751 Sorry I am not quite clear what you mean by "if you measure the population mean 100 times", but I think there are some good answers and explanations below as to what confidence intervals are. — Stefan, Aug 17 '20 at 16:27
@Stefan PedroSebe's answer points out that the parameter is not the random variable. I never considered that some people might think it was. Those people might think that 95% of parameters are contained within the confidence interval, not vice versa. — user253751, Aug 17 '20 at 16:30
@user253751 Correct, in frequentist statistics the parameters are fixed and not considered random variables for a given experiment. Say you have a distribution with mean $\mu$ and standard deviation $\sigma$, than these are the parameters of this distribution and hence are fixed. Now you take a sample from this distribution and calculate a confidence interval based on the sample data. At this point we don't know whether $\mu$ is in this particular interval - but we know that if we repeat sampling a very large number of times under the exact same conditions ... — Stefan, Aug 17 '20 at 16:50
...we get a very larger number of confidence intervals which will, in the case of a 95% confidence interval, contain $\mu$ in 95% of all calculated confidence intervals. This is what I tried to get across in my answer. However, you should also note that in Bayesian statistics the parameter is considered to be a random variable and hence a probability distribution can be generated that allows to make probabilistic statements about the parameter! — Stefan, Aug 17 '20 at 16:50

PedroSebe · Answer 1 · 2020-08-17T15:13:43.570

Is this wording incorrect? It seems to be saying that the true value has a 95% chance of being in that specific confidence interval.

You have to keep in mind that, in frequentist statistics, the parameter you are estimating (in your case $\beta_i$, the true value of the coefficient) is not considered as a random variable, but as a fixed real number. That means it is not correct to say something like "$\beta_i$ is in the interval $[a,b]$ with $95\%$ probability", because $\beta_i$ is not a random variable and therefore does not have a probability distribution. The probability of $\beta_i$ being in the interval is either $100\%$ (if the fixed value $\beta_i\in[a,b]$) or $0\%$ (if the fixed value $\beta_i\notin[a,b]$)

That is why "95% confidence interval means there is a 95% chance that the true parameter falls in this range" is a misconception.

On the other hand, the limits of the confidence interval themselves are random variables, since they are calculated from the sample data. That means it is correct to say "in 95% of all possible samples, $\beta_i$ is in the 95% confidence interval". It does not mean that $\beta_i$ has $95\%$ chance of being inside a particular interval, it means that the confidence interval, which is different for each sample, has $95\%$ probability of falling around $\beta_i$.

Notice that the confidence interval will contain $\beta_i$ with 95% probability before the data is sampled. After it is sampled, the confidence intervals edges will be just two fixed numbers, not random variables anymore and the same rationale from the first paragraph applies. I think the following image offers a nice visualization to this idea:

Therefore, the wording used there is actually correct.

Aside from using 95% to get the 1.96 Z-score, how else is the 95% manifested in this confidence interval?

The 1.96 Z-score is the only place where the 95% shows up. If you change it for the Z-score corresponding to, say, 85%, you would have the formula 85% confidence interval.

In "of all possible samples," what does "samples" refer to here? — user5965026, Aug 16 '20 at 05:33
Frequentist stats and confidence intervals do not necessarily treat the coefficient as an unknown constant. It can be just as well a variable and it may often be the case. And also, even if it is considered a constant, it is perfectly fine to speak about the probability that 'the constant is within some interval' (Or if you feel uncomfortable with this expression then you can turn it around and say, the probability that 'the interval is around the constant') Even if the parameter is constant, the interval is not, thus it is fine to make probability statements about relations between the two. — Sextus Empiricus, Aug 16 '20 at 15:16
@SextusEmpiricus about the "point being in interval" thing: agreed, the point I was trying to make is that it doesn't make sense to discuss the probability of a fixed interval containing a fixed constant. So, for instance, if I evaluate my confidence interval to be (0,3), I cannot say there's 95% probability that the parameter falls in there, since it is now a fixed interval. On the other hand, *before* I evaluate the confidence interval, it is a random variable and I can make probabilistic assertions about it, as you said. — PedroSebe, Aug 17 '20 at 15:20
@PedroSebe before or after the measurement, the interval remains a variable. Just like I describe in the urn model at the end of my answer. **The (confidence) interval is *not* a fixed interval (it shares this property with any other type of interval) , it is a variable depending on the observations** — Sextus Empiricus, Aug 17 '20 at 16:11
Fundamentally I disagree with you that $\beta_i$ is "not a random variable". Mathematically randomness has always referred to *uncertainty* about the value of the variable. For instance, if someone flips a coin but keeps the result hidden from you, it's still valid to say that the result is 50% heads. Even though the coin has already been flipped and either IS heads or tails, its result is still random to you due to your uncertainty. — Brady Gilg, Aug 17 '20 at 18:08

Stefan · Answer 2 · 2020-08-16T21:56:18.403

8

Perhaps if you rephrase to:

"Imagine you repeat your sampling under the exact same conditions indefinitely. For each draw you calculate a parameter estimate and its standard error in order to calculate a 95% confidence interval [formula in your figure]. Then this 95% confidence interval will capture the true population parameter in 95% of the time if all assumptions are met and the null hypothesis is true."

Would that make more sense?

As for you second question, consider the standard normal distribution below. The total area under the curve equals to 1. If you consider the significance level to be 5% and split this up between each tail (red areas), then you are left with 95% in the middle. If the null hypothesis is true then this is the area in which you would not reject the null hypothesis as any Z-score that falls in that area is plausible under the null hypothesis. Only if your Z-score falls into the red areas, you reject the null hypothesis, since your sample provides significant evidence against the null hypothesis, or in other words you likely made a discovery - hooray :D

Now by multiplying the critical Z-score of +/-1.96 (in case of 95% confidence) with the standard error of the sample you are translating this 95% interval back onto the original measurement scale. So each confidence interval corresponds to a hypothesis test on your measurement scale as suggested in the last sentence on your image.

edited Aug 16 '20 at 21:56

answered Aug 16 '20 at 05:43

Stefan

4,977
1
18
38

Yes, I think this makes sense. I was actually also confused what "samples" in "95% of all samples" of the original quote was referring to. It seems the "samples" here is referring to all the confidence intervals, or the sets of data used to generate those confidence intervals? – user5965026 Aug 16 '20 at 05:49
1

@user5965026 Yes, correct. Since you can calculate a confidence interval from each sample, you will end up with as many confidence intervals as you have samples (and none of those will be exactly the same). As this number gets very large, the 95% confidence interval will contain the true population parameter in 95% of those confidence intervals. – Stefan Aug 16 '20 at 05:58
Based on Sedro's answer below, it seems the following is also correct to say "The confidence interval has a 95% chance of containing the true value," but the following "There is a 95% chance that the true value is in the confidence interval." It reads very similarly, and I think the difference in these 2 statements are really subtle. – user5965026 Aug 16 '20 at 06:13
@user5965026 yes the chance aspect relates to the confidence interval and not the parameter. The parameter is unknown but **fixed**. So the 95% confidence interval is jumping around the true parameter and if you generate a very large number of these confidence intervals then in 95% of the cases it has contained the parameter. – Stefan Aug 16 '20 at 06:34

score 1 · Answer 3 · answered Aug 17 '20 at 20:35

1

95% conf.int. means there is only a 5% chance that actual empirical value falls out of this interval. In other words, 5% chance of false positive if (and when) you treat that range as ground truth.

answered Aug 17 '20 at 20:35

ivan866

121
5

Sextus Empiricus · Answer 4 · 2020-08-18T07:45:40.430

My second question is, say you have one of these 95 confidence intervals. Aside from using 95% to get the 1.96 Z-score, how else is the 95% manifested in this confidence interval?

The 95% is manifested in the following way

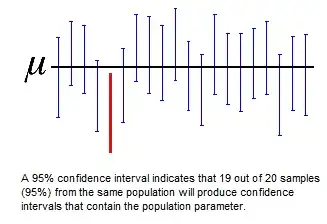
Probability statement: "95% confidence interval means there is a 95% chance that the true parameter falls in this range"

There are misconceptions about this statement, but the statement itselve is not a misconception.

Whether or not the probability statement is true depends on how you condition the probability. It depends on the interpretation of what is meant by probability/chance.

You can express this probability 'the interval containing the true parameter' conditional on the observation but also conditional on the true parameter.

So yes, the probability statement is wrong if the probability is wrongly interpreted.

But no, the probability statement is not wrong if the probability is correctly interpreted.

Example

from https://stats.stackexchange.com/a/481937/ and https://stats.stackexchange.com/a/444020/

Say we measure $X$ in order to determine/estimate $\theta$

$$X \sim N(\theta,1) \quad \text{where} \quad \theta \sim N(0,\tau^2)$$

Here $\theta$ follows a distribution as well. (You can imagine for instance that $\theta$ is some measure of intelligence which differs from person to person where $N(0,\tau^2)$ is the distribution of $\theta$ among all persons. And $X$ is the result from some intelligence test).

Below is a simulation of 20k cases.

In the image we draw lines for the borders of a 95% confidence interval (red) and a 95% credible interval (green) as a function of the observation $X$. (For more details about the computation of those borders see the reference)

We can consider 'the probability of an interval containing the true parameter' as conditional on the observation $X$ or conditional on the true parameter $\theta$. We have plotted the two different interpretations for both type of intervals. Only in the right one (conditional on $X$), the probability statement about the confidence interval is false.

.

Practical situation that explains the relevance of this view: Say in the above example, which could be about an intelligence test, we have done the test in order to select people with high intelligence, and we have a sub sample of people that tested with a specific range of test observation $X$ (e.g. we selected candidates with a high intelligence for some job). Now we may wonder for how many of these people their 95% confidence interval contains the true parameter.... well, it won't be 95% because the confidence interval does not contain the parameter in 95% of the cases when we condition on a particular observation (or range of observations).

Misconceptions about the misconception

It is often mentioned that the probability statement is not true because after the observation the statement is either 100% true or 0% true. The parameter is either in or outside the interval and it can not be both. But we do not know which of the two cases it is, and we express a probability for our data-based certainty/uncertainty about it (based on some assumptions).

(Note that this argument about 'the probability statement being false' would work for any type of interval, but somehow because the confidence interval relates to a frequentist interpretation of probability the probability statement is disallowed.)

It is perfectly fine to speak about the probability that 'the parameter is within some interval' (Or if you feel uncomfortable with this expression then you can turn it around and say, the probability that 'the interval is around the parameter') Even if the parameter would be a constant, the interval is not a constant (but a random variable), thus it is fine to make probability statements about relations between the two. (and if this argument is still not comfortable then one could also adopt a propensity probability interpretation instead of a frequentist interpretation of probability, a frequentist interpretation is not necessary for confidence intervals)

Example: from an urn with 10 red and 10 blue balls you 'randomly' pick a ball without looking at it. Then you could say that you have 50% probability to have picked red and 50% to have picked blue. Even though in the (unknown) reality it is either 100% blue or 100% red and not really a random pick but a deterministic process.

Pedantic notes

The interval that contains the true value $\beta_i$ in 95% of all samples is given by the expression...

Is this wording correct?

It is not the interval. There will be multiple intervals with the same property.
More specifically it is an interval that contains the true value $\beta_i$ in 95% of all samples independent from the true value of $\beta_i$

I find this answer somewhat confusing and hope you could clarify this a bit further. In frequentist statistics aren't we always condition the sample on a fixed parameter value, $P(data|hypothesis)$, with respect to null hypothesis testing? Isn't the reverse, i.e. $P(hypothesis|data)$ what defines the posterior probability in Bayesian statistics? — Stefan, Aug 16 '20 at 16:14
From my understanding credible intervals are a Bayesian construct whereas confidence intervals are a frequentist construct. The former treats the hypothesis as a random variable conditioned on the data, the latter treats the data as random and conditions on a fixed parameter. I have yet not seen any statistical analysis that follows the frequentist approach, i.e. providing p-values and such, and also calculating credible intervals, i.e. intervals that describe the probability of the parameter given the data. So depending on how you condition depends on frequentists vs Bayesian, no? — Stefan, Aug 16 '20 at 16:35
OK, so I guess the part I don't understand is when do you treat the parameter as not fixed in a frequentist confidence interval setting? A reference to a paper that uses such a confidence interval or a text book that mentions this would be great. On the Wikipedia page on [confidence intervals](https://en.wikipedia.org/wiki/Confidence_interval) I cannot seem to find this interpretation either. Thank you! — Stefan, Aug 16 '20 at 17:19
Sorry you lost me here in this thick forest of statistical terminology. Maybe I can borrow your machete? I mean it is clear that the parameter can change form experiment to experiment but for one given experiment it is fixed since the null hypothesis assumes that the realized sample was drawn from a data generating process with **fixed** parameters. — Stefan, Aug 16 '20 at 18:33
Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/111869/discussion-between-sextus-empiricus-and-stefan). — Sextus Empiricus, Aug 17 '20 at 07:07
This answer is just plain false. It is treating the question as a philosophical one. This is not Philosophy SE, this is Cross Validated SE. Within standard frequentist statistics, which the question specifically asked about, probability does *not* refer to a quantity merely being unknown. In frequentist statistics, "Take a 20 sided die and roll it. If it comes up 1, say that your confidence interval is the null set. Otherwise, say that it's the entire real line." is a technically valid (albeit extremely useless) method of creating a 95% confidence interval. — Acccumulation, Aug 17 '20 at 21:37
@Acccumulation, the question does not ask about 'within frequentist statistics'. The OP does not mention this at all. — Sextus Empiricus, Aug 17 '20 at 23:05
@Acccumulation I am not treating the question as philosophical (although maybe it should be treated like that and [philosophy](https://stats.stackexchange.com/questions/tagged/philosophical) would not be wrong on SE). I am even giving a *practical* example which explains how the probability statement ( "95% confidence interval means there is a 95% chance that the true parameter falls in this range") can be wrong. And I give another example explaining that the way how it is often considered wrong is wrong. — Sextus Empiricus, Aug 17 '20 at 23:06
Yes, take a fair 20 sided dice. The probability that you do not roll 1 is 95%. How is that a false probability statement? What is your point? — Sextus Empiricus, Aug 17 '20 at 23:06
@acccumulation I have edited my introduction. I believe that you are right that given a particular instance of the (useless) confidence interval (null set or whole set) it would be weird to say that the parameter is inside the interval with 95% probability. This is because for this particular construction we *know* the probability *conditional* on the confidence interval. The parameter is outside if you rolled the dice 1 and outside if you did not roll 1..... — Sextus Empiricus, Aug 18 '20 at 07:53
.... an alternative to your example. Let some parameter be a number between 1 and 20 (but we do not know which). Let a confidence interval/set be made by rolling a 20 sided dice and take the numbers 1 to 20 with the number from the dice roll excluded. Then if we rolled the dice the same as the unknown parameter then our CI is wrong and in the other potential 95% cases the CI is right. ..... — Sextus Empiricus, Aug 18 '20 at 07:58
....That is a similar useless confidence interval as yours but now we do not know the probability of the parameter inside the interval *conditional* on the confidence interval. But we can express the probability of the parameter inside the confidence interval conditional on the parameter, just like we can express probabilities of outcomes from an urn model (The probability that two dice rolls are the same, why can we express that probability but we aren't allowed to do this for confidence intervals which can be modelled analogously?). — Sextus Empiricus, Aug 18 '20 at 08:01

Is 95% specific to the confidence interval in any way?

4 Answers4

Example

Misconceptions about the misconception

Pedantic notes