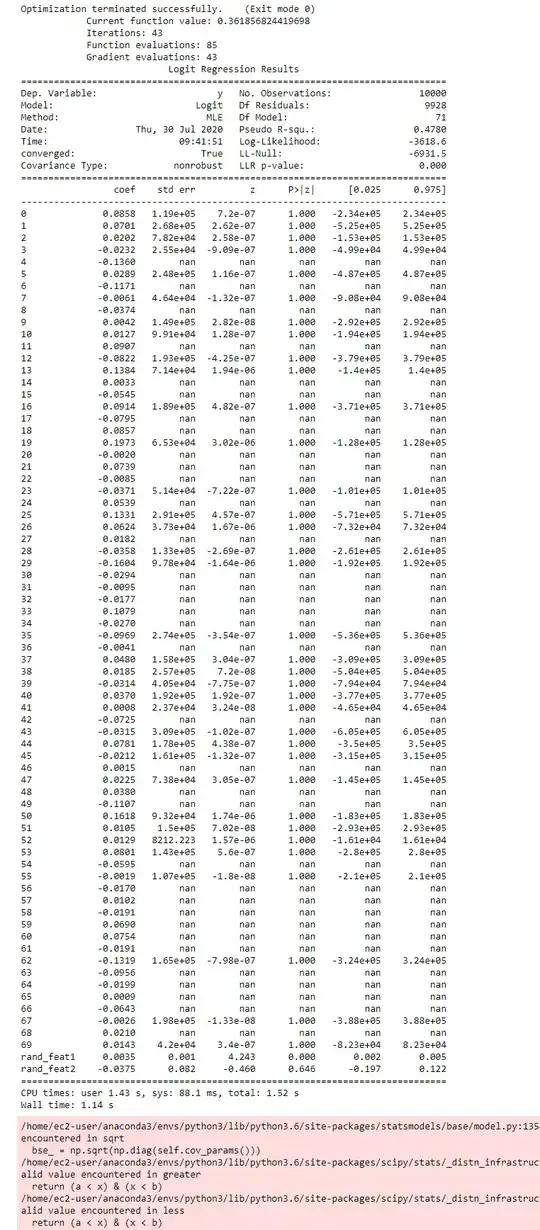
I keep getting warnings such as
RuntimeWarning: invalid value encountered in greaterreturn (a < x) & (x < b)
and my model summary is full of nans and very large standard errors. The model performance is near identical with what I get when I train with sklearn so it works fine for predictions. But why am I seeing so many weird numbers? I've seen answers about perfect separation causing similar issues - but that is not the case here? I've seen with real data but I get the same issues with generated data as well.
Code to reproduce
import statsmodels.api as sm
import pandas as pd
from sklearn import datasets
from numpy import random
data = datasets.make_classification(n_features = 70, n_informative = 50, n_redundant = 20,n_samples= 10000, random_state = 3)
X = pd.DataFrame(data[0] )
y = data[1]
X['rand_feat1'] = random.randint(100, size=(X.shape[0]))
X['rand_feat2'] = random.randint(100, size=(X.shape[0]))/100
logit_model=sm.Logit(y, X)
sm_result=logit_model.fit_regularized(maxiter = 10000)
print(sm_result.summary())
Output: