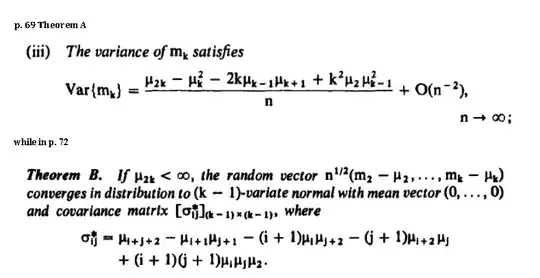In "Serfling, R. J. (1980). Approximation theorems of mathematical statistics", we read
In Theorem A, as one suspects, $k=1,2,...$, indicating the integer-moments, while $n$ is the sample size. As regards the $m_k$ and $\mu_k$ symbols, we have, drawing i.i.d from the distribution of some random variable $X$,
$$m_k = \frac 1n \sum_{i=1}^n (X_i-\bar X)^k, \;\;\;\mu_k = E[(X-E(X)]^k$$
Theorem A is concerned with each separate central sample moment, Theorem B is concerned with their joint limiting distribution.
Suppose that $k=3$. Then, from Theorem A we have
$$\text{AVar}(m_3) = \mu_6 - \mu_3^2 - 6\mu_2\mu_4 + 9\mu_2^3$$
But from Theorem B, setting $i=j=3$ we get
$$\text{AVar}(m_3) = \mu_8 - \mu_4^2 - 8\mu_3\mu_5 + 16\mu_3^2\mu_2$$
I don't see how the two can coincide, and some quick simulated checks show that they don't.
Question:is it possible that the expression in Theorem B is meant only for the off-diagonal covariance terms and not for the diagonal variance terms?
The author makes no such clarification.