5

If I have two groups, one with a sample size of, say, 700,000 observations and another with 10,000 observations and I want to test the difference between the means of the two groups, what would be the best way to go about it?

  1. Using Welch's t-test because it is not affected by unequal variances (which usually show up because of the difference in sample sizes).
  2. Taking a random sample from the '700,000' group? (a random sample of 10k observations). I took 1000 samples of 10k from the bigger group and the p-value was always <0.05. But another interesting thing I read somewhere that p-values are always low if the data sample size is really big.
  3. Any better way of doing it?

Also, will the Welch's t-test results be untrustworthy because of the underlying skewed distributions?

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
Vardayini
  • 53
  • 4
  • 1
    **Not true** that the P-value is always low for large sample sizes. If there really is a difference, a large sample will increase the probability of detecting that. But if there is no difference, a large sample won't 'invent' one for you. Example in R: `set.seed(12); x = rnorm(1000,100,10); y = rnorm(1000,100,12)` `t.test(x,y)$p.val` returns P-value 0.1664101. – BruceET Aug 08 '20 at 00:18
  • 1
    1) Why do you say that the unequal variance shows up due to unequal sample sizes? 2) Do you mean Welch’s t-test as opposed to the equal- variance t-test? – Dave Aug 08 '20 at 01:28
  • @BruceET Thanks for the example, I shouldn't have stated it like a fact. What I meant by that was that because of the larger sample size the test would be sensitive to the smallest of difference. Maybe using something like Cohen's d would help look at the extent of the effect? – Vardayini Aug 09 '20 at 08:25
  • @Dave 1) I'm a newbie, so I read on a lot of answers that the assumption of equal sample sizes is there to say that approx. the variances are equal in the two groups. 2) Yes, I mean Welch's t-test. my bad, I'll update the question. – Vardayini Aug 09 '20 at 08:28
  • Your last paragraph seems to be the only place you refer to "underlying skewed distributions". With pronounced skewness, even whether t tests of any flavour are a good idea could be at issue. Other way round, if skewness here is a slip for unequal spread, please fix the question. – Nick Cox Aug 09 '20 at 10:17

1 Answers1

3

If you have data on $n_1 = 700,000$ in Group 1 and $n_2= 10,000,$ then I wonder about two issues:

(a) Unbiasedness. Were the observations randomly taken in order to represent the groups fairly? Or are they self-selected subjects who may not be representative. On the positive side, are these samples so large that they essentially exhaust their respective populations--perhaps making issues of sampling bias are less important.

(b) Descriptive or testing approach. With such large samples, it may be sufficient to show summary statistics, data tables, or graphical descriptions of the data. If you feel testing is important, then what would be the point of taking a subsample of the larger group? Doing that to "even up" the sample sizes is not necessary because test accommodate to unequal sample sizes. Doing that to improve "randomness" is futile: if the large sample is unrepresentative of the population, then a small subsample can be no better.

If data in the two groups are approximately normal, then a Welch two-sample t test with the sample sizes $n_1$ and $n_2$ will not be spoiled by unequal sample sizes or by unequal population variances. As mentioned above test results may not tell you anything you don't already know from descriptive statistics, but the test procedure itself should introduce no fresh difficulties.

You briefly mention that the data are skewed. Without further information it is difficult to say whether skewness would be invalidate the t test even with these large sample sizes. (If skewness is severe and is similar between the two distributions, it may be better to use a two-sample Wilcoxon (rank sum) test. Due to lack of information, I am ignoring this issue for now.)

Here are two simulated datasets of sizes $n_1$ and $n_2$ with a small, but noticeable difference in means and unequal variances.

set.seed(2020)
x1 = rnorm(700000, 103, 15)
x2 = rnorm(10000,  100, 20)

summary(x1)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  32.59   92.91  102.99  103.02  113.12  175.41 
summary(x2)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  28.32   86.68  100.10   99.89  113.25  176.54

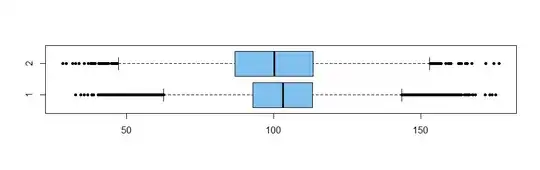
The sample mean and median of the larger sample are larger than the sample mean and median, respectively, of the smaller sample. Boxplots show the medians, and give a clear impression that values in the larger sample are somewhat larger than those in the smaller sample. The boxplot also shows greater variability for the first sample. [Ordinarily, one would make the boxplot for the larger group thicker than the other one, but the difference seemed distracting here.]

boxplot(x1, x2, col="skyblue2", names=c(1,2), 
        pch=20, horizontal=T)

enter image description here

The test gives a reasonable answer. The P-value is very nearly $0$ so there is little question of statistical significance. Also, a 95% confidence interval $(2.74, 3.52)$ for the difference $\mu_1 - \mu_2$ in sample means is convincingly far from including $0.$

t.test(x1, x2)

        Welch Two Sample t-test

data:  x1 and x2
t = 15.771, df = 10164, p-value < 2.2e-16
alternative hypothesis: 
  true difference in means is not equal to 0
95 percent confidence interval:
 2.740895 3.518955
sample estimates:
mean of x mean of y 
103.02070  99.89077

Note: A Wilcoxon rank sum test also shows significance for my simulated data:

wilcox.test(x1, x2)$p.val
[1] 1.130024e-64
BruceET
  • 47,896
  • 2
  • 28
  • 76
  • Thank you so much! This is really helpful. I have a few followup questions: a) under unbiasedness, the samples are from observed data. For eg, Imagine I'm taking the visit frequency of users who buy a product and users who do not buy a product from a website in a given time period. Aren't these users inherently random? – Vardayini Aug 09 '20 at 08:46
  • b) Following the descriptive approach, the means, say, were 10 and 9. But how do we know that the difference between the 10 and 9 was significant and not a random variance? Because there were some extreme values, the boxplots were only helpful when I removed the extreme values, but is it right to do so? C)I was previously using Wilcoxon rank-sum test, but it gave me significant results even though the median of the two groups was the same. After further reading, I realized that for large datasets they are not accurate as it also indicates the difference in spread. – Vardayini Aug 09 '20 at 08:46
  • 1
    (+1) Careful, well-crafted answer as always. The boxplot works well in your example but it's worth underlining that it shows medians and quartiles, not any quantities directly relevant to a t-test of any flavour. – Nick Cox Aug 09 '20 at 10:14
  • 2
    The Wilcoxon test tests a more general hypothesis of whether values from one population tend to be larger than values from the other population. When such stochastic ordering is of interest, then use the Wilcoxon test and don't worry so much about variances or skewness. Or consider the Kolmogorov-Smirnov two-sample test (difference in two cumulative distribution functions). In general, if you want to go parametric, you may need a 4-parameter skew t-distribution for your data. – Frank Harrell Aug 09 '20 at 10:53
  • 1
    (a) Buying or not buying is hard to model. Depends on circumstances (hand sanitizer in pandemic), season (wooly sox in winter), trendiness (black nail polish--who knows why or for how long). Careful description may be best. (b) Nuking far outliers is almost always wrong. For I-commerce they might be major story. (c) Right that Wilcoxon test is not just a t test for when you worry about non-normal data. @FrankHarrell's suggestion on K-S test worth considering, but possibly challenging to implement / interpret With whatever test, think hard about what its _saying_ not just what you want to know. – BruceET Aug 09 '20 at 13:15
  • Thanks for the suggestions! One thing, I noticed after taking mean of samples from the two groups, the resulting distributions are normal. Then I can ignore the skewness of the original distribution because the T-test assumes the distribution of the means and not the population to be normal? – Vardayini Aug 10 '20 at 06:10
  • No, the t-test assumes that the raw data are normal. That's how the standard deviation and mean are independent of each other which makes the t distribution be the right one to use for the t statistic. You are intimating the central limit theorem, which **in the limit** helps to maintain the type I assertion probability $\alpha$ but has nothing to do with maintaining good statistical power. – Frank Harrell Aug 10 '20 at 10:54
  • @FrankHarrell: I see, but I found a different point of view here under the first answer: https://stats.stackexchange.com/questions/9573/t-test-for-non-normal-when-n50/9781 – Vardayini Aug 14 '20 at 08:07
  • That answer is quite incorrect on that one point. Suppose the raw data come from a skewed distribution. Then the mean and SD are not independent and the statistic no longer follows a t distribution. And the CLT completely ignores type II error (1 - power). – Frank Harrell Aug 14 '20 at 16:29
  • @FrankHarrell: Wholeheartedly agree with you that t tests are not as 'robust' against non-normality as often claimed, and for the exact reason you mention. Moreover, I did say, "If data in the two groups are approximately normal, then..." (Just in case the context of your last comment gets lost.) – BruceET Aug 14 '20 at 16:50
  • 1
    Just don't say that the t-test just needs the means to be approximately normally distributed. That's not nearly enough. – Frank Harrell Aug 14 '20 at 21:26
  • Thank you for clarifying that. What would be a good resource to learn about distributions and these assumptions that one must keep in their minds while deciding on a test? I do not have a background in statistics and want to make my concepts clear as I read many different opinions online @FrankHarrell – Vardayini Aug 14 '20 at 21:48
  • The problem is that a mantra has developed about the robustness of t methods, saying (roughly) they are fine by the CLT, unless there is marked skewness or far outliers, but in any case OK if $n\ge 30.$ This has been endlessly repeated--especially (not exclusively) in elementary psych, soc, and biostat texts--and is quite wrong. For every correct reference on the topic, someone can find a dozen conflicting "authorities" who have mindlessly copied the mantra from elsewhere without verification. – BruceET Aug 14 '20 at 21:58
  • 1
    There are several posts on these issues on this site. These are very common misconceptions. If you have a log normal distribution the CLT may be bogus for up to n=50,000. Read papers by Rand Wilcox. – Frank Harrell Aug 14 '20 at 22:01