The formula for Baye's rule is as follows $$p(\theta |D) = \frac{p(D|\theta)p(\theta)}{\int p(D|\theta)p(\theta)d\theta}$$
where $\int p(D|\theta)p(\theta)d\theta$ is the normalising constant $z$. How is $z$ evaluated to be a constant when evaluating the integral becomes the marginal distribution $p(D)$ ?
$p(D)$ is a constant with respect to the variable $\theta$, not with respect to the variable $D$.
Think of $D$ as being some data given in the problem and $\theta$ as the parameter to be estimated from the data. In this example, $\theta$ is variable because we do not know the value of the parameter to be estimated, but the data $D$ is fixed. $p(D)$ gives the relative likelihood of observing the fixed data $D$ that we observe, which is constant when $D$ is constant and does not depend in any way on the possible parameter values $\theta$.
Addendum: A visualization would certainly help. Let's formulate a simple model: suppose that our prior distribution is a normal distribution with mean 0 and variance 1, i.e. $p(\theta) = N(0, 1)(\theta)$. And let's suppose that we're going to observe one data point $D$, where $D$ is drawn from a normal distribution with mean $\theta$ and variance 1, i.e. $p(D | \theta) = N(\theta, 1)(D)$. Plotted below is un-normalized posterior distribution $p(D | \theta) p(\theta)$, which is proportional to the normalized posterior $p(\theta | D) = \frac{p(D | \theta) p(\theta)}{p(D)}$.
For any particular value of $D$, look at the slice of this graph (I've shown two in red and blue). Here $p(D) = \int p(D | \theta) p(\theta) d\theta$ can be visualized as the area under each slice, which I've also plotted off to the side in green. Since the blue slice has a larger area than the red slice, it has a higher $p(D)$. But you can clearly see that these can't currently be proper distributions if they have different areas under them, since that area can't be 1 for both of them. This is why each slice needs to be normalized by dividing by its value of $p(D)$ to make it a proper distribution.
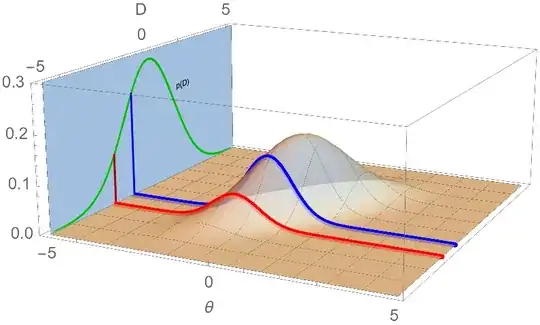
The normalising constant in the posterior is the marginal density of the sample in the Bayesian model.
When writing the posterior density as $$p(\theta |D) = \frac{\overbrace{p(D|\theta)}^\text{likelihood }\overbrace{p(\theta)}^\text{ prior}}{\underbrace{\int p(D|\theta)p(\theta)\,\text{d}\theta}_\text{marginal}}$$ [which unfortunately uses the same symbol $p(\cdot)$ with different meanings], this density is conditional upon $D$, with $$\int p(D|\theta)p(\theta)\,\text{d}\theta=\mathfrak e(D)$$ being the marginal density of the sample $D$. Obviously, conditional on a realisation of $D$, $\mathfrak e(D)$ is constant, while, as $D$ varies, so does $\mathfrak e(D)$. In probabilistic terms, $$p(\theta|D) \mathfrak e(D) = p(D|\theta) p(\theta)$$ is the joint distribution density of the (random) pair $(\theta,D)$ in the Bayesian model [where both $D$ and $\theta$ are random variables].
The statistical meaning of $\mathfrak e(D)$ is one of "evidence" (or "prior predictive" or yet "marginal likelihood") about the assumed model $p(D|\theta)$. As nicely pointed out by Ilmari Karonen, this is the density of the sample prior to observing it and with the only information on the parameter $\theta$ provided by the prior distribution. Meaning that, the sample $D$ is obtained by first generating a parameter value $\theta$ from the prior, then generating the sample $D$ conditional on this realisation of $\theta$.
By taking the average of $p(D|\theta)$ across values of $\theta$, weighted by the prior $p(\theta)$, one produces a numerical value that can be used to compare this model [in the statistical sense of a family of parameterised distributions with unknown parameter] with other models, i.e. other families of parameterised distributions with unknown parameter. The Bayes factor is a ratio of such evidences.
For instance, if $D$ is made of a single obervation, say $x=2.13$, and if one wants to compare Model 1, a Normal (distribution) model, $X\sim \mathcal N(\theta,1)$, with $\theta$ unknown, to Model 2, an Exponential (distribution) model, $X\sim \mathcal E(\lambda)$, with $\lambda$ unknown, a Bayes factor would derive both evidences $$\mathfrak e_1(x) = \int_{-\infty}^{+\infty} \frac{\exp\{-(x-\theta)^2/2\}}{\sqrt{2\pi}}\text{d}\pi_1(\theta)$$ and $$\mathfrak e_2(x) = \int_{0}^{+\infty} \lambda\exp\{-x\lambda\}\text{d}\pi_2(\lambda)$$ To construct such evidences, one need set both priors $\pi_1(\cdot)$ and $\pi_2(\cdot)$. For illustration sake, say $$\pi_1(\theta)=\frac{\exp\{-\theta^2/2\}}{\sqrt{2\pi}}\quad\text{and}\quad\pi_2(\lambda)=e^{-\lambda}$$ Then $$\mathfrak e_1(x) = \frac{\exp\{-x^2/4\}}{\sqrt{4\pi}}\quad\text{and}\quad\mathfrak e_2(x) = \frac{1}{1+x}$$ leading $$\mathfrak e_1(2.13) = 0.091\quad\text{and}\quad\mathfrak e_2(2.13) = 0.32$$ which gives some degree of advantage to Model 2, the Exponential distribution model.
I think the easiest way to figure out what's going on is to think about how you might approximate the integral.
We have $p(\mathcal{D}) = \int p(\mathcal{D}|\theta) p(\theta) \rm d \theta$.
Note that this is just the average of the likelihood (first term in the integrand) over the prior distribution.
One way to compute this integral approximately: sample from the prior, evaluate the likelihood, repeat this lots of times and average the results.
Because the prior and the dataset are both fixed, the result of this procedure doesn't depend on the value of $\theta$. $p(\mathcal{D})$ is just the expected likelihood under the prior.
Why is the normalisation constant in Bayesian not a marginal distribution?
The normalisation constant is a marginal distribution.
"How is $z$ evaluated to be a constant when evaluating the integral becomes the marginal distribution $p(D)$"
The integral provides indeed a probability density of the observations ($D$ can be any value). So $z$, or better $z(D)$, is a function of $D$.
But when you evaluate $z(D)$ for a particular given observation $D$ then the value is a constant (a single number and not a distribution).
$$p(\theta |D) = \frac{p(D|\theta)p(\theta)}{\int p(D|\theta)p(\theta)d\theta} = \frac{p(D|\theta)p(\theta)}{p(D)}$$
Note that the posterior $p(\theta |D)$ is a function of $D$. For different $D$ you will get a different result.
