Classifier can predict time series 1 day in advance, but not more. Why?

Question

To ask the question more precisely: when doing Time Series classification, I observe the classifier prediction is good if test data directly follows (in chronology) the train data. But when the train and test sets are separated in time (even by very small amount of records), the performance falls dramatically fast. Is this the expected behavior? Below are all the details:

I am working on timeseries classification. My timeseries data describe certain events in time. I have about 60 events (records) daily. These events have about 30 features and a binary label: 0/1. I need to predict this label.

The typical ratio of 1/0 is roughly 0.3/0.7, so essentially on an average day I expect 20 ones and 40 zeros. Thus the classes are unbalanced (imbalanced). I have 84 days of data that can be used as train/test. This maps to 5,000 records.

My classifier is XGBoost, because in several previous experiments it worked best. I also understand that it performs well in unbalanced set scenarios. I also make sure the records are sorted chronologically and that train and test sets are correctly split and separated in time: the train set is always before test set. The success metrics is F1_score (both precision and recall are important).

Now, the problem is as follows:

After many experiments I have gotten to reasonable results: F1 = .73, with classifier trained on 2500 records (40 days of data). This is an average number, because the same classifier tested on different test days will of course yield variable results. And here lies the issue. I wanted to see how exactly these results differ between particular test days. By examining closer these daily results, I saw they were not uniform: the results were much better if the tested day directly followed the train set. For instance (Diagram 1 below), when the train set consisted of data from 15 May-15 June, then the classifier would perform best on 16 June's data and then rapidly fall.

I suspected this was to do with the data, especially that the ratio of C1 class (shown by dotted line on diagrams) was slightly different on various days. So I fixed this, by purposely downsampling the test data, day by day, to the same ratio that the train set had (about 0.3, as stated earlier). I then run more tests and saw that this phenomenon was not specific to any particular day, but happened always.

Diagram 2 shows the classifier trained on 1000 records (16 days) of data, and then tested on 28 days that follow directly the test set. So, the train + test batch had the total of 44 days of data. This experiment has then been repeated 40 times: First covering the beginning (initial 44 days) of the available 84-day data set, and then each time the train+test batch has been shifted by 1 day into the future. So eventually all the data was covered. Diagram 2 below shows the averaged results. Now the trend is clear and the hypothesis confirmed: the results (precision and recall) are always better on day following the test set, regardless of the date (or day of week). Then they systematically drop, especially the recall

Diagram 3 shows the same experiment, with different parameters: classifier trained on 3,000 records (48 days of data), tested on 10 days, and the experiment repeated 26 times (note I don't have more data: 48 + 10 + 26 = 84). We can see that the results are somewhat better (because the classifier had more data for train), but the trend persists: the performance is always best on the day following the train set.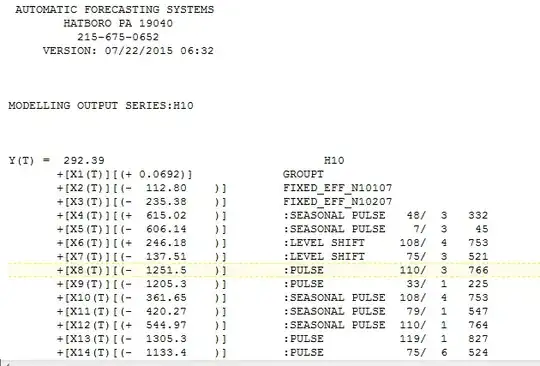

While this behavior can be accepted in general, I feel something is very wrong here. I understand that the data may change over time (data drift) and so the performance of predictions are generally expected to worsen with time. But the rate of this is too fast. For example, have a look how quickly Recall (sensitivity) drops, in Diagram 3: I trained the classifier over 48 days. Then, if tested on day 49, recall is 0.61, but tested only 5 days later it drops below 0.4. My naive reasoning is this: given that the train period was 48 days, the test data variability, if any, should not be so dramatically visible to confuse the classifier so quickly.

But the experiments prove otherwise. I feel I am doing something wrong. A methodology error? Any hints or ideas welcome.

Edit4.8.2020: To clarify even more, I want to explain the meaning of the data. My data describe events (technical incidents) that happen in the certain network infrastructure. 1 record = 1 incident, e.g. a hard drive crash. The label (target) 0/1 means importance. In great simplification, an event is important (1) if it is likely to cause more trouble in near future if not fixed immediately. We know which events in the past turned to be important (they indeed did cause more trouble later on), and those have been labelled 1. So, the business goal of the classification is to distinguish important events (1) from unimportant ones (0) early in the game, and pass this information to the team who then prioritizes the fixing work accordingly. As stated, on an average day we have 20 important events and 40 unimportant ones.

Answer 1

I found the answer thanks to the thoughtful comments by @Pawel and @Tim. Their both suggested that there must be an implicit close chronological relationship between the data located closely in time, so that yesterday test data (part of train) may be related to today's data (part of test). This was key inspiration, allowing me to discover the problem.

The problem was in the label (target variable). As explained in the post, the meaning of the label 1 was that an event was important, meaning: it will cause problems in the future. Yes, future... Events labelled 1 were those that had documented causal effect up to 7 days in advance. So the label had implicitly allowed the classifier to peak up to 7 days in the future.

And here is how it worked: when test set was very close to train set, the classifier could cheat, because the test events labelled 1 were similar or even identical to the very recent train events, which it has already seen and learned. Separating the train and test sets by 7 days made that cheating impossible, so the performance dropped.

I may be able to post more when the solution has been documented, for now just this quick explanation to let everyone know what the nature of the problem was. @Pawel and @Tim, thank you. Very impressive insight.

Answer 2

Isn't it that testing on data that follows directly the train data is almost like testing on train dataset? I mean, depending on the nature of your data but probably there is a small difference between train data on day x and test data on day x+1 and that is why you have good results at the beginnig.