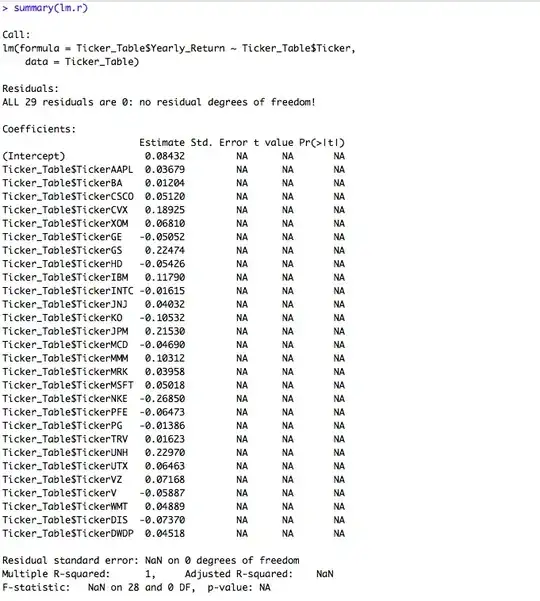
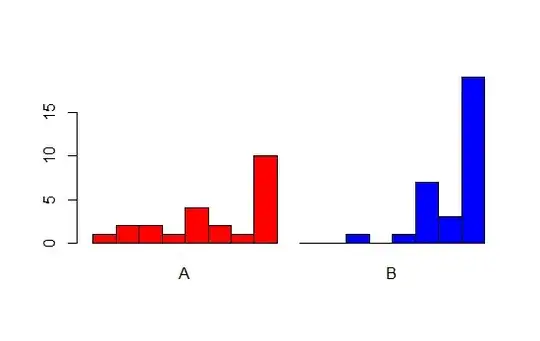
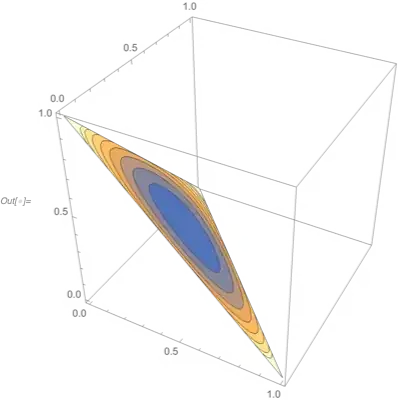
It is said that the distribution with the largest entropy should be chosen as the least-informative default. That is, we should choose the distribution that maximizes entropy because it has the lowest information content, allowing us to be maximally surprised. Surprise, therefore, is synonymous with uncertainty.
Why do we want that though? Isn't the point of statistics is to estimate with minimal error or uncertainty? Don't we want to extract the most information we can from a dataset/random variable and its distribution?