If teachers account for 30% of variance of student achievement, can a teacher have 30% increase in achievement by teaching better?

Question

My professor wrote:

Research using sophisticated statistical techniques indicates that teaching expertise accounts for about 30 percent of the variance in student achievement (Hattie, 2003). Think about what your student test scores would look like if you could achieve this 30 percent increase with each group of students that passed through your classes each year.

I believe the professor misunderstands variance accounted for. "Teaching expertise accounts for about 30 percent of the variance in student achievement" means that a teacher is responsible for 30% of what a student achieves. You can't infer from this that a great teacher will achieve a 30% increase in student achievement relative to... a teacher who didn't teach at all? If we had 2 teachers, one at the bottom of teaching expertise and the other at the top, teach classes which had all other variables constant (socioeconomics, motivation, etc.), would the better teacher's class achieve a 30% increase relative to the worse teacher?

Answer 1

You are right in suspecting that your professor misunderstood.

The correct answer is that we cannot say anything whatsoever about the percentage improvement in student achievement driven by teacher expertise. Nothing at all.

Why is this so? The quote is in terms of variance explained. Variance explained has nothing to do with the actual values on which the scales are measured - which any percentage improvement in student achievement would be accounted in. The two are completely separate.

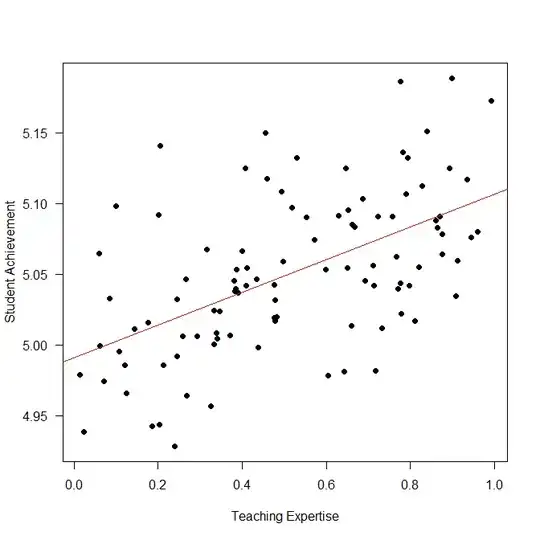
Let's look at an example. Here is some simulated data:

R code:

nn <- 1e2
set.seed(1) # for reproducibility

teaching_expertise <- runif(nn)
student_achievement <- 5+0.1*teaching_expertise+rnorm(nn,0,0.05)
model <- lm(student_achievement~teaching_expertise)

plot(teaching_expertise,student_achievement,pch=19,las=1,
    xlab="Teaching Expertise",ylab="Student Achievement")
abline(model,col="red")

Note that the model is correctly specified: student achievement depends linearly on teaching expertise, and that is what I am modeling. No cheap tricks here.

We have $R^2=0.30$, so teaching expertise indeed accounts for 30% of student achievement (see here):

> summary(model)

Call:
lm(formula = student_achievement ~ teaching_expertise)
... snip ...
Multiple R-squared:  0.304,     Adjusted R-squared:  0.2969

However, here is the student achievement we would predict for teachers at the very bottom (teaching expertise of 0) vs. at the very top of the range (1):

> (foo <- predict(model,newdata=data.frame(teaching_expertise=c(0,1))))
       1        2 
4.991034 5.106651

The improvement is on the order of $\frac{5.11-4.99}{4.99}\approx 2.4\%$.

> diff(foo)/foo[1]
         2 
0.02316497

(Plus, this is expected achievement. Actual achievement will be different. With regression to the mean typically being stronger at the extremes, the actual difference will be even smaller.)

And you know what? We could change this percentage change to pretty much any number we want. Even a negative percentage improvement! How? Simply by changing that single innocuous number 5 in the data simulation above, i.e., the intercept.

What's going on? Variance explained measures the amount by which the (sum of squared) residuals are reduced by a model, i.e., the difference between the residuals to the regression line and the residuals to the overall average. By changing the intercept (the 5), we can shift everything up and down. Including the overall average. So changing the intercept will leave variance explained completely unchanged. (If you have R, try this. We'll wait.)

However, shifting everything up and down will change the concrete scores. In particular the percentage improvement of a "good" vs. a "bad" teacher. If we shift everything down far enough, we get a negative student achievement for the "bad" teacher. And a positive change for the "good" teacher against a negative baseline will give you a negative percentage improvement. (Again, try this. An intercept of -1 works.)

Yes, of course such negative percentage improvements make no sense here. This is just an illustration of the fact that there is zero relationship between variance explained and percentage improvement in measurements.

Answer 2

The Hattie 2003 paper mentions a simple form of hierarchical linear modelling ignoring interactions. The paper’s description of the 30% isn’t particularly thorough, with broken links in the references making it difficult to see where the number even came from. I assume his approach relied on partial R-squared.

The answer is no, going from a bad teacher to a good teacher can’t be expected to increase performance by 30%. The two 30%'s are measured completely differently.

For example, suppose performance followed this equation:$$\text{performance} = \beta_0 + \beta_1 ~\text{studentEffort} + \beta_2 ~\text{teacherEffort} + \text{noise}$$If the $\beta_2$ is small, the performance graph would be nearly flat as teacherEffort changed. This can happen no matter what the $R^2$ is or how it might divide up into partial $R^2$'s.

In other words, saying that teachingEffort accounts for 30% of a variation doesn't tell you what that variation is over the dataset, i.e. how much performance changes.

Answer 3

You write '"Teaching expertise accounts for about 30 percent of the variance in student achievement" means that a teacher is responsible for 30% of what a student achieves.'

A better formulation would be "A teacher is responsible for 30% of the difference in performance between students".

In other words, if the average performance of some group of students with teacher A is 80 points and the average performance of another group with teacher B is 70 points, the performance of the teachers A and B can account for around 3 points (30% of the 10 point variance in performance).