In short
The simplified case, with spherically symmetric $\boldsymbol{\eta}$ (that is i.i.d $\eta_j \sim \mathcal{N}(0,\sigma)$), can be related to a transformed non-central t-distribution.
We have:
$$ \sqrt{n-1} \frac{\rho}{\sqrt{1-\rho^2}} \sim T_{\nu = n-1, ncp = l/\sigma} $$
where $l$ is the length of the vector $\mathbf{X}$.
Geometric view of problem, and rotation
We can view the problem by considering the radial and transverse components of the distance of the vector $Y$. These transverse and radial components are defined with respect to the vector $X$.
This means that the direction of $\mathbf{X}$ is not really important, because we consider the situation relative to $\mathbf{X}$
This view is easier when we rotate the vector $\mathbf{X}$ such that it is aligned allong one single axis. For instance, in the code below we generate/simulate samples with the vector $\mathbf{X}$ having only the first component non zero, $\lbrace l,0,0,\dots,0,0 \rbrace$. We can do this without loss of generality.
In the case that $\boldsymbol{\eta}$ has i.i.d. $\eta_j \sim \mathcal{N}(0,\sigma)$, then the distribution will be spherically symmetric. This means that after the rotation the distribution of the rotated $\boldsymbol{\eta}$ can still be considered to have i.i.d. components.
See the image below where we rotate the situation (to align the vector $\mathbf{X}$ to a basis vector). On the left we see the situation for the complex situation (not all $\eta_j$ identical but with different variance) and on the right we see the situation for the simplified case.
Now we can attack the problem by focussing on the angle, $\phi$, between $\mathbf{X}$ and $\mathbf{Y}$. The actual direction of $\mathbf{X}$ does not matter, and we can parameterize the distribution by only the length of $\mathbf{X}$, say $l$.
The angle $\phi$ can be described by its cotangent, the ratio of the the radial and transverse parts of the vector $Y$ relative to $X$.
Note that, with the rotated vector $\mathbf{X} \sim \lbrace l, 0, 0, \dots, 0, 0 \rbrace$ the components of $\mathbf{Y}$ are easier to express
$$Y_i \sim \begin{cases} N(l,\sigma)\quad \text{if} \quad i=1 \\ N(0,\sigma)\quad \text{if} \quad i\neq 1\end{cases}$$
and we can easily express the radial part, $Y_1$, and the transverse part, $\lbrace Y_2,Y_3, \dots, Y_{n-1}, Y_{n} \rbrace$. And the lengths will be distributed as:
The length of the radial part is a Gausian distributed variable
The length of the transverse part is a scaled $\chi_{n-1}$ distributed variable.
(The image is in 2D for simplicity of plotting, but you should imagine this in a multidimensional way. The length of the transverse part is a sum of $n-1$ components. A similar construction is shown here where a 3D visualization of the angle is shown)
This ratio of the radial and transverse part, multiplied with $\sqrt{\nu}$, lets call it $T_{l/\sigma,nu}$, has a t-distribution with non-centrality parameter $l/\sigma$ and degrees of freedom $\nu = n-1$ (were $n$ is the dimension of your vectors).
note: this t-distribution occurs because the radial part and transverse part are independently distributed in the simplified problem. In the generalized problem this will not work (although the limit, large $n$, may still be useful when we appropriately adapt the scaling factor). See this in the first image on the left, where after rotation the distribution of $Y$ shows a correlation between transverse and radial part, and also the transverse part is not anymore $\sim \chi_{n-1}$, because the individual component may have different variance.
The transformation between $T_{l/\sigma}$, which is the cotangent of the angle (multiplied with $\sqrt{\nu}$), and your dot product $\rho$, which is the cosine of the angle is:
$$\rho = \frac{T_{l/\sigma}}{\sqrt{\nu+T_{l/\sigma}^2}}$$
$$T_{l/\sigma} = \sqrt{\nu} \frac{\rho}{\sqrt{1-\rho^2}}$$
If $f(t,\nu,l/\sigma)$ is the non-central distribution (which is a bit awkward to write down, so I just write it as $f$), then the distribution $g(\rho)$ for the dotproduct is
$$g(\rho) = f\left(\sqrt{\nu} \frac{\rho}{\sqrt{1-\rho^2}},\nu,l/\sigma\right) \frac{\sqrt{\nu}}{(1-\rho^2)^{3/2}}
$$
That distribution is a bit difficult to write down. It might be easier to work with a transformed correlation coefficient
$$ \sqrt{n-1} \frac{\rho}{\sqrt{1-\rho^2}} \sim T_{\nu = n-1, ncp = l/\sigma} $$
For large $n$ this will approximate a normal distribution.
Simulation
l = 10
sig = 2
n = 10
set.seed(1)
simulate = function(l, sig , n) {
eta <- rnorm(n, mean = 0, sd = sig)
X <- c(l,rep(0,n-1))
Y <- X + eta
out1 <- (Y %*% X)/sqrt(X %*% X)/sqrt(Y %*% Y) # this one is rho
out2 <- sqrt(n-1)*Y[1]/sqrt(sum(Y[-1]^2)) # this is related non central t-distributed
c(out1,out2)
}
rhoT <- replicate(10^4, simulate(l,sig,n))
rho <- rhoT[1,]
t <- rhoT[2,]
# t-distribution
hist(t,breaks = 20, freq = 0)
ts <- seq(min(t),max(t),0.01)
lines(ts,dt(ts,n-1,ncp=l/sig))
# distribution of rho which is transformed t
hist(rho, freq = 0, breaks = seq(0,1,0.01))
rhos <- seq(-0.999,0.999,0.001)
lines(rhos,dt(x = rhos*sqrt(n-1)/sqrt(1-rhos^2),
df = n-1,
ncp = l/sig)*sqrt(n-1)/(1-rhos^2)^1.5)
Non simplified problem
In this case the $\boldsymbol{\eta}$ is not symmetric and the view of the ratio of a horizontal and vertical part (relating to a t-distribution) does not work so well. The two parts may be correlated and also the vertical part is not anymore chi-distributed but will be related to a sum of the square of correlated normal distributed variables with different variance.
However, I guess that for large dimension $n$ we may expect that the transformed variable will approach again a normal distribution (but the scale factor depending on the degrees of freedom $\nu=n-1$ may need to be adapted).
Below is a simulation that demonstrates this:
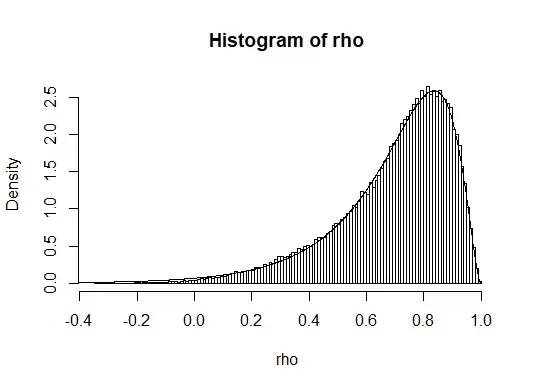
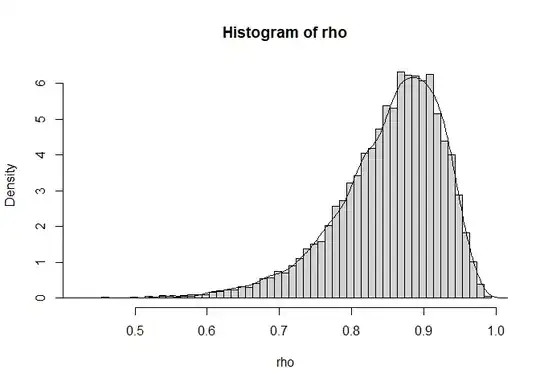
These simulations indicate that a t-distribution still fits well, but we need to use a different effective scaling, different non-central parameter and different degrees of freedom. In the image the curve is drawn based on fitting those parameters. I believe that it will be difficult to find exact expressions for these parameters, but I guess that it is safe to say that it will still be approximately a transformed non-central t-distribution.
#### defining parameters
###
set.seed(1)
n = 10
l = 10
sigspread = 3 ### the higher this number the smaller the spread of the different sigma
sig = 2*rchisq(n,sigspread)/sigspread
X <- rnorm(n,1,1)
### make the vector X equal to size/length "l"
lX <- sqrt(sum(X^2))
X <- X*(l/lX)
### function to simulate a sample and compute the different statistics
### rho, the radial and transverse parts and the cotangent which is related to rho
simulate = function(l, sig , n) {
eta <- rnorm(n, mean = 0, sd = sig)
Y <- X + eta
out1 <- (Y %*% X)/sqrt(X %*% X)/sqrt(Y %*% Y) # this one is rho
radial <- (Y %*% X)/sqrt(X %*% X)
transverse <- sqrt(sum(Y^2)-radial^2)
out2 <- sqrt(n-1)*radial/transverse # this is related to rho and non central t-distributed
c(out1,out2,radial,transverse)
}
### simulate a sample to make the histogram
rhoT <- replicate(10^5, simulate(l,sig,n))
### the simulated values
rho <- rhoT[1,]
t <- rhoT[2,]
radial <- rhoT[3,]
transverse <- rhoT[4,]
### fitting of the transformed variable
hfit <- hist(rho/(1-rho^2)^0.5, breaks = 100, freq = 0)
yfit <- hfit$density
xfit <- hfit$mids
### fitting
mod <- nls(yfit ~ dt(xfit*scale, nu, ncp)*scale,
start = list(nu = n-1, ncp = l/sqrt(mean(sig^2)), scale = sqrt(n-1)),
lower = c(1,0,0.1),
upper = c(n*2, l/sqrt(mean(sig^2))*2,10), algorithm = "port")
coef <- coefficients(mod)
### curve which is naive initial guess
lines(xfit, dt(xfit*sqrt(n-1),
df = n-1,
ncp = l/sqrt(mean(sig^2))
)*sqrt(n-1), col = 2 )
### curve which is fitted line
lines(xfit, dt(xfit*coef[3], df = coef[1], ncp = coef[2])*coef[3], col = 4 )
### plotting rho with fitted value
h <- hist(rho, freq = 0, breaks = 100)
rhos <- seq(-0.999,0.999,0.001)
lines(rhos,dt(x = rhos/(1-rhos^2)^0.5*coef[3],
df = coef[1],
ncp = coef[2])/(1-rhos^2)^1.5*coef[3])
### initial estimates
c(nu=(n-1),
ncp = l/sqrt(mean(sig^2)),
scale = sqrt(n-1))
### fitted values
coef
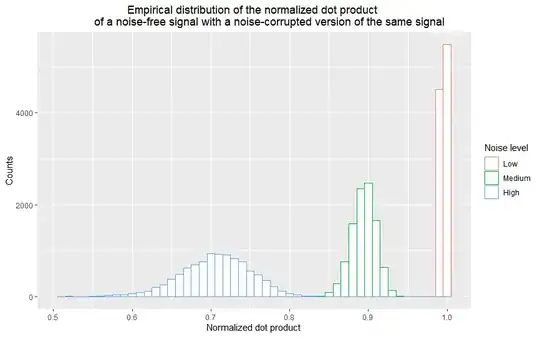 $10,\!000$ noise realizations and computed the normalized dot product between each noisy signal and the noise free signal" />
$10,\!000$ noise realizations and computed the normalized dot product between each noisy signal and the noise free signal" />