2

Is there any theorem which states the asymptotic distribution for the sample mean when the samples are drawn from a random variable which has a bounded interval?

Ben Rozemberczki
  • 21
  • 3
  • 2
    To be brief, the central limit theorem is about $z=\sqrt{n}\dfrac{\bar{x}-\mu}{\sigma}$ converging to $N(0,1)$, not about $\bar{x}$ converging. In fact, $\bar{x}$ converges to $\mu$ by the law of large numbers. – Dave Jul 17 '20 at 01:30
  • 3
    But, to be less brief and also correct: as $Z_n = \frac{\bar X - \mu}{\sigma/\sqrt{n}}$ approaches _standard normal_ the distribution of $\bar X$ _does_ become normal with appropriate mean and SD. – BruceET Jul 17 '20 at 09:37

1 Answers1

1

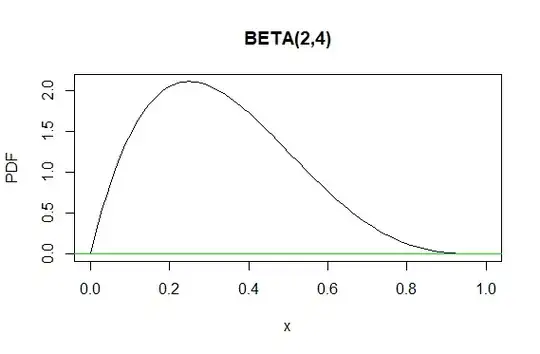
Beta distributions have support $(0,1).$ Here is the density function for $\mathsf{Beta}(2,4),$ which has $\mu=1/3,\sigma^2=2/63.$ [Using R.]

curve(dbeta(x,2,4), 0, 1, ylab="PDF", main="BETA(2,4)")
abline(h=0, col="green2")

enter image description here

Averages of even small samples from this distribution are nearly normal. The boundedness prevents extreme values and so convergence of the Central Limit Theorem is relatively rapid. The simulation below shows the approximate distribution of samples of size $n = 20$ from this distribution (histogram). The red density curve is for the best-fitting normal distribution $\mathsf{Norm}(1/3, 0.03984).$

set.seed(2020)
a = replicate(10^5, mean(rbeta(20, 2, 4)))
mean(a)
[1] 0.3331668    # aprx 1/3
sd(a)
[1] 0.0398627    # aprx 0.3984
sqrt(2/(63*20))
[1] 0.03984095   # exact SD

hdr = "n=20: Sample Means for BETA(2,4)"
hist(a, prob=T, br=50, col="skyblue2", main=hdr)
 curve(dnorm(x, mean(a), sd(a)), add=T, col="red")

enter image description here

BruceET
  • 47,896
  • 2
  • 28
  • 76