0

I want to perform a bootstrap/simulation of the significance of a KS test in some observed data and have come up with some synthetic examples to make sure my code works, which I base off Greg Snow's answer here, off Clauset et al. 2009's approach, and off Colin Gillespie's poweRlaw package. The real data follows a truncated lognormal distribution, for reference. I don't see any questions that cover exactly what I do here. I want to be sure my approach and code are correct, given the observation on the histogram of p-values at the end.

Say I have some values, X, of length N, I know follow a given distribution, say lognormal, but I don't know the parameters, theta. I estimate the parameters using MLE, theta_est, and then compute the KS-statistic, KS_est, of the fitted distribution. Now I want to evaluate the goodness of fit but I know that the Kolmogorov distribution is biased in the case of estimated parameters. I turn to simulation and do the following.

 For M simulations: 
   simulate N lognorm values with parameters theta_est. 
   alternative 1: compute KS-statistic of simulated data (KS_sim1) & p-value using theta_est. 
   alternative 2: Estimate new parameters for simulated data, theta_hat, and then compute KS_sim2 using theta_hat. 
end

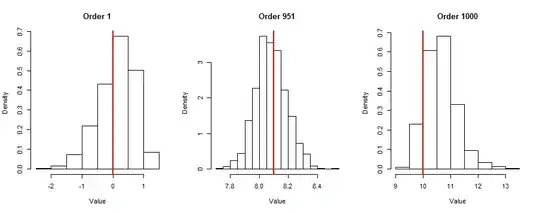
Alternative 2 is the 'correct' way according to Clauset, Greg Snow's answer, other answers from Glen_b, unless I am mistaken. I do this, and I find that the CDF of KS_sim1 and the Kolmogorov distribution (KS_analytical) closely match each other, while the CDF of KS_sim2 is shifted to the left and much steeper. This means that the estimated p-value [ P(KS_est > KS_sim) ] is much lower for KS_sim2 and for KS_analytical. I want to believe alternative 2, but then I check the histogram of simulated p-values, and find that the histogram is uniform for alternative 1 but not for alternative 2! Where is my mistake? In fact the p-value histogram is very skewed for alternative 2. Is it because I am computing the p-value from KS_analytical? Any insight, and recommended reading would be greatly appreciated.

library(fitdistrplus)
library(kolmim)
randlnorm <- rlnorm(1000, 4, 1)
hist(randlnorm,breaks="FD")
plot(ecdf(randlnorm))

flnorm <- fitdistrplus::fitdist(randlnorm, 'lnorm')

pv <- ks.test(randlnorm, 'plnorm', meanlog = flnorm$estimate[1], sdlog = flnorm$estimate[2])

lnorm_sim_KS <- sapply(1:2500, function(i) {
  randlnorm_sim <- rlnorm(length(randlnorm), meanlog = flnorm$estimate[1], sdlog = flnorm$estimate[2])
  flnorm_sim <- fitdistrplus::fitdist(randlnorm_sim, 'lnorm')
  
  pv_sim <- ks.test(randlnorm_sim, 'plnorm', meanlog = flnorm$estimate[1], sdlog = flnorm$estimate[2])
  pv_sim2 <- ks.test(randlnorm_sim, 'plnorm', meanlog = flnorm_sim$estimate[1], sdlog = flnorm_sim$estimate[2])
  
  return(c(pv_sim$statistic, pv_sim$p.value, pv_sim2$statistic, pv_sim2$p.value))
})


KS_toeval <- seq(.001, .05, by = .001)
Fks_anal <- kolmim::pkolmim(KS_toeval, length(randlnorm))


# CDF of KS
plot(KS_toeval, Fks_anal, xlim = c(0, 0.05), type = "l",
     ylim = c(0, 1), lwd = 3, main = bquote(F[x]*(KS)), xlab = "KS-statistic",
     cex.lab = 1.6, cex.axis = 1.6, cex.main = 1.6, ylab = bquote(F[x]))
grid(lwd = 2, col = rgb(0.05, 0.05, 0.05, 0.5))
lines(ecdf(lnorm_sim_KS[1, ]), lwd = 3, col = "blue")
lines(ecdf(lnorm_sim_KS[3, ]), lwd = 3, col = "red")
legend("topleft", lwd = 3, lty = 1, col = c('black', 'blue', 'red'),
       legend = c('Analytical Kolmogorov', 'const. par sim.', 'est. par sim.'))

abline(v= pv$statistic, lwd = 3, lty = 2)


par(mfrow=c(2, 1))
hist(lnorm_sim_KS[2, ], xlab = "p-val alternative 1")
hist(lnorm_sim_KS[4, ], xlab = "p-val alternative 2")



> mean(lnorm_sim_KS[1, ] >= pv$statistic)
[1] 0.602
> mean(lnorm_sim_KS[3, ] >= pv$statistic)
[1] 0.178
> pv$p.value
[1] 0.5938039

enter image description here enter image description here

Heymans
  • 21
  • 4
  • Can you explain what your code is intended to do in the second approach, please. The problem with doing it with code us that it conflates errors of understanding (implementing the wrong idea) with errors of implementation (incorrectly implementing the right underlying idea), making the job of people trying to understand what you're doing more difficult – Glen_b Jul 11 '20 at 05:42
  • Good point. In alternative 2, for each iteration we estimate the parameters of the target distribution in from the simulated data. This is in line with Greg Snow's answer here: https://stats.stackexchange.com/questions/45033/can-i-use-kolmogorov-smirnov-test-and-estimate-distribution-parameters and what is outlined in Clauset et al. 2009 (save for their x_min section). As I understand it, the idea is because we don't know the parameters, so we should replicate the estimation procedure to somehow incorporate the parameter estimation error into the KS statistic distribution. – Heymans Jul 11 '20 at 05:53
  • I also saw your answer here https://stats.stackexchange.com/questions/111693/simulation-of-ks-test-with-estimated-parameters but do not fully understand part 3. What do you mean by treat the estimated parameters as the population value and then compute the KS statistic as it simplifies the computation? Can we not simply compute the ks statistic between the simulated data and estimated parameters of the simulated data? – Heymans Jul 11 '20 at 06:02

0 Answers0