3

I am a graduate student in animal science. I am comparing linear models that fit covariates of var1 and var2. These two covariates are decomposed from one quantity say F (inbreeding level of animal).

I decomposed F based on the cut-off number of generations in the pedigree used to define new inbreeding, e.g., 5, 10, 15 generations. For 5 generations, F = Fnew_5 + Fold_5, etc. My purpose is to just determine which cut-off threshold that is the best among candidates.

I want to compare model performance using different sets of var1 and var2.

y = mu + fixed_effects + b1var1 + b2var2 + e

where, y is body weight of animal, fixed_effects include sex, birth_year, age at measure. I chose to fit a fixed linear regression model due to its simplicity and my familiarity. I want to compare model performance (Aj.R2, RMSE, AIC, BIC) across all different ways to decompose the inbreeding F.

Results are:

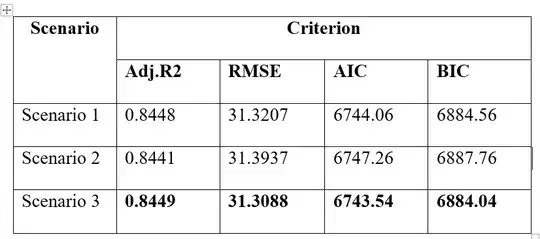
enter image description here

In this case, scenario 3 showed slightly better than scenario 1 and 2 across all criteria.

My question is that does the model ranking change if I add another random effect (like animals) in the model? This random effect will be the same for all different models.

In other word, If I want just to see what is the best cut-off threshold to decompose inbreeding (F) in to new and old F, is fixed effect model sufficient to do so?

Thank you.

Pattrapoljk Sumreddee
  • 33
  • 5
  • Hi welcome to the site. Why do you want to decompose A What is A ? Please give some examples of the different way you do this. What is the outcome and the other fixed effects ? Please explain a bit more about your research and your research questions. Just edit your question to add the information. – Robert Long Jul 10 '20 at 18:11
  • Thank you @RobertLong I have added the requested information. – Pattrapoljk Sumreddee Jul 10 '20 at 22:36

1 Answers1

4

My question is that does the model ranking change if I add another random effect (like animals) in the model? This random effect will be the same for all different models.

It might, because the estimation procedures are different In mixed effects models. However this should not deter you from using mixed models. They are often the best solution when you have a lot of subjects. Also, you can fit random slopes, if supported by the data. If you don't use mixed models and you have multiple subjects then you either need to fit subject ID as a random intercept in a mixed model, fit fixed effects (which will be inconvenient if you have many subjects) or use another method such as GEE.

Also note that R^2 is not defined for mixed models. There have been attempts to create pseudo R^2 but they don't have the same properties as in linear models so consequently if you use them you may obtain conflicting results. Save yourself some trouble and don't use R^2 for mixed models.

Robert Long
  • 53,316
  • 10
  • 84
  • 148