Reconstruction Error: Principal component analysis vs Probabilistic prinicpal component analysis

Question

I am working through the book "Machine Learning: A Probabilistic Perspective". After introducing PCA and Probabilistic PCA, the following graphic is shown (the upper two graphics correspondend to PCA and the lower two to PPCA, rmse = root mean squared error, all plots visualize the reconstruction error):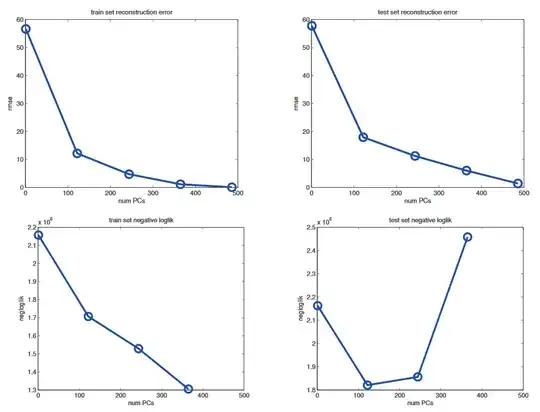

The arising question is:

Why has PCA not the typical Bias-Variance-Trade off U-Shape, but PPCA does?

The explanation in the book is the following:

The problem is that PCA is not a proper generative model of the data. It is merely a compression technique. If you give it more latent dimensions, it will be able to approximate the test data more accurately. By contrast, a probabilistic model enjoys a Bayesian Occam’s razor effect (Section 5.3.1), in that it gets “punished” if it wastes probability mass on parts of the space where there is little data. (i.e. one should pick the simplest model that adequately explains the data.)

Summing up and my question:

I think why PCA does not have a U-Shape is clear. The latent variables are the number of eigenvectors we consider. The more we take, the better we approximate the data. So no magic is done.

However, I don't manage to fully understand the behavior of PPCA. I thought that PPCA almost equals PCA if the noise $\sigma$ of the data vanishes. So I don't understand why there is then such a different behavior?

Thanks in advance if someone could explain this in detail! :)

Answer 1

I can hazard an answer here, but I think you're right to be confused.

To recap what you've said, the difference is in the criteria to evaluate predictions about the test set.

PCA uses RMSE, which simply evaluates how close the reconstructed data $\hat X$ is to the original data $X$ when encoded using $L$ components.

PPCA uses (negative) log-likelihood of the original data, given the reconstruction and the estimated noise ($\sigma$), $-log[ P(X | \hat X, \sigma)]$. As discussed in Section 5.3.1 of your textbook, the likelihood penalises the model both for errors in the value of $\hat X$, and for how widely it spreads the probability mass --- that is, for high values of $\sigma$, which can account for many values of $X$ but aren't very specific about which to actually expect.

---

I strongly suspect the decrease in log-likelihood with $L > 100$ is due to changes in the estimate of $\sigma$, either causing it to be underestimated (model is overconfident in the reconstructed values) or overestimated (under-confident). I can't say whether it's systematically guaranteed to be one or the other, but you could easily check on a case-by-case basis.

Answer 2

I'll give you an intuitive answer about why PCA and PPCA are different.

I'll put aside the dimensionality reduction purpose for both the techniques.

PCA is a method to define a new space vector which basis (PCA loadings) are characterised by the property:

• the projection of the data $X$ along the $i$-th loading has maximum retained variance

This shows clearly that PCA is not a model for the dataset $X$ (it's not a parametric representation, usually approximated). On the contrary, PCA simply defines a new vector space (which basis are the PCA loadings - remember that they are orthonormal and form a complete basis for the original feature space) such that the variance explained by projection is maximal. As a consequence, when using the entire set of principal components to represent the data, you have the same original data points of $X$. Equivalently, increasing the number of dimensions of this new vector space, you get a more accurate approximation of the original data.
When using the entire set of loadings, one just represents the original data points with a new orthonormal basis. For this reason, as one increases the number of PCA loadings, the original space gets represented more accurately and consequently also the training and test data. The reconstruction error for the training and test data may have different slopes, but both go to zero.

Probabilistic PCA instead is, as the name says, a "probabilistic" model of the data. As described here, PPCA assumes the following factor model

$$ \mathbf{x=Wz+\mu+\epsilon}\\ \mathbf{\epsilon}\sim N(\mathbf{0}, \sigma^2 \mathbf{I})\\ \mathbf{x|z} \sim N(\mathbf{Wz+\mathbf{\mu}},\sigma^2 \mathbf{I}) $$

where $\mathbf{x}$ represents the observations, $\mathbf{z}$ the latent variables, and $W$ represents the loadings. Differences from PCA: 1) these assumptions are not always accurate, 2) the parameters of $\mathbf{x|t}$ depend on the training set. In general, as one increases the number of parameters of the model (the number of principal components), one gets more accurate reconstruction of the training set, but at the same time the deviations from the assumptions affect more significantly the generality of the model (overfitting). In PPCA, data will always be modelled as Normally distributed (or a different generative distribution), in PCA, there's no such assumption.

The key point is that the figures for PPCA don't show the reconstruction error, but log-likelihood trends. These are calculated from the assumed Normal model, and they show how the estimated parameters get affected by the specificity of the training observations.

Under the condition of normality, however, PCA and PPCA are similar and they become identical when $\sigma^2\rightarrow 0$.