1

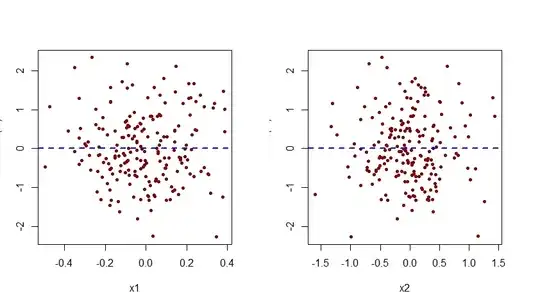
I am trying to perform a normality test to multiple continuous values before doing an anova test. The p-value I am getting for the data does not make much sense and I want to make sure I am not missing something.

  • My data consists of 40k rows, I cannot use scipy.stats.shapiro so I am using kstest
  • When doing a shapiro test I believe the W value has to be close to 1. Does the same apply to D statistic value?
  • most p-values are 0.0 which makes me think I am missing something.
  • What values from the kstest will render the anova results valid?
  • Should I be using Anderson-Darling test given that the data is not normally distributed? if so would it still count as a normality test?
  • I tried converting some columns from lognorm to norm by doing df['income'] = df['income'].apply(lambda x: math.log10(x)) that seem to result in p-values that approach zero. but I am not sure if that's the right method. if it is, should the anova analyze the log(income) as well or it does not matter?

here is the code I used to do the test:

from scipy.stats import norm, kstest

for var in numerical_features:
    loc, scale = norm.fit(df[var].to_numpy())
    n = norm(loc=loc, scale=scale)
    d, p = kstest(df[var].to_numpy(), cdf=n.cdf)
    print("{0} {1} {2}".format(var, d, p))

Here is the data itself:

age: D=0.054 p=9.488e-84

age

income: D=0.142 p=0.0

income

vehicles owned: D=0.409 p=0.0

cars

years of experience: D=0.175 p=0.0

years

Kirill Kulakov
  • 113
  • 3

1 Answers1

1

Well you hardly need a test to tell you that your data are not normally distributed. If you take a quick look at your histograms you can directly see that. Moreover if you have a large sample size as you do you will almost by definition reject the $H_0$ of normality even if your data is very close to being normally distributed (see e.g. here on CV). Thus your small p-values are simply a result of 1) the fact that your data is indeed not normal distributed and 2) you have a very large sample size.

More to the point however is if you need normality of your data (see e.g. this related question). ANOVA is pretty robust, so violation of normality is not always a problem, especially for large sample sizes where we can rely on the central limit theorem (see among others again here and here).

If you do decide to transform your data to have it conform to the normality, then indeed you need to do the ANOVA on the transformed data. Keep in mind though, that comparing the means of income is not exactly the same as comparing the log of income, so this will affect your results (see here)

Maarten Punt
  • 683
  • 5
  • 11