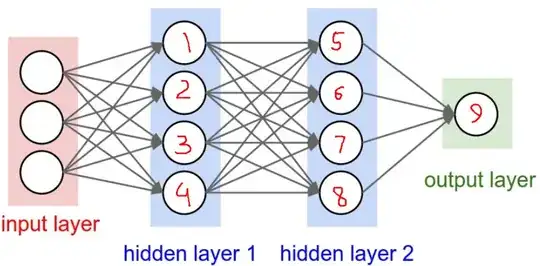
Since my last question on the topic I have tried searching on my own how zero weight initialization impedes learning but I can't quite seem to wrap my head around the concept. The CS231n course notes explain that zero-initializing the weights is a bad idea because
[...] if every neuron in the network computes the same output, then they will also all compute the same gradients during backpropagation and undergo the exact same parameter updates.
I am unable to understand this explanation. I understand the first bit, that all the neurons will compute the same output in the forward pass. However, I don't see why the gradient flowing back would be the same?
For example, take the network below. Say the gradient flowing back to Hidden Layer 2 from the output layer is $a$. In Hidden Layer 2, this upstream gradient would get multiplied by the local gradient, say $b$, to get the gradient $ba$ on this layer's weights. Next, these gradients will flow back to Hidden Layer 1, and if the neurons in Hidden Layer 1 also have a local gradient of $b$, then the gradient on Hidden Layer 1's weights would come out to be $b^2a$. I might be overlooking some detail here, but if this reasoning is right by any chance, then it seems like different gradients are flowing through the network. From the output layer we have $a$ flowing back, from Hidden Layer 2 we have $ba$ flowing back, and from Hidden Layer 1 we have $b^2a$ flowing back. But according to the course notes, the gradients flowing back should be the same
Edit
I was also wondering why symmetry breaking is called so? I am confused why the network is said to be "symmetrical" if all the neurons have the same outputs. I guess one can assume the network to be symmetrical about the longitudinal axis of the network; but that is just me guessing. I have so far not found any sources on how the term came about