Relationship between overfitting and robustness to outliers

Question

What's the relationship between overfitting and sensitivity to outliers? For example:

• Does robustness to outliers make necessarily models less prone to overfitting?
• What about the other way around? Are models that are less prone to overfitting usually more robust to outliers?

Or do these concepts bear no relationship at all?

---

Noise driving overfitting and outliers

Consider for example this definition in Wikipedia:

"The essence of overfitting is to have unknowingly extracted some of the residual variation (i.e. the noise) as if that variation represented underlying model structure", that suggests a deeper connection between noise and overfitting.

So clearly some form of noise plays a role in overfitting. Similarly, one often models outliers as noise that the model may generate, i.e. it's something you can protect yourself against by using a noise model that would explain outliers with e.g. fat tail distributions.

So maybe the relationship here comes down to what type of noise we are fighting against in overfitting vs outliers? And if so, what is a good definition of these types of noise, and what's their relationship?

Answer 1

Interesting questions posed. I will address the two questions for the use case of statistical classifiers in order to demarcate the analysis to a model domain we can oversee.

Before embarking onto an elaborate answer I do want to discuss the definition of Robustness. Different definitions have been given for the concept of robustness. One can discuss model robustness - as opposed to outcome robustness. Model robustness means that your general model outcome - and hence the distribution of its predictions - that they are less sensitive or even insensitive to an increasing amount of extreme values in the training set. Outcome robustness, on the other hand, refers to the (in)sensitivity to increasing noise levels in the input variables with respect to one specific predicted outcome. I assume that you address model robustness in your questions.

To address the first question, we need to make a distinction between classifiers that use a global or local distance measure to model (probability of) class dependency, and distribution-free classifiers.

Discriminant analysis, k-nearest neighbor classifier, neural networks, support vector machines - they all calculate some sort of distance between parameter vectors and the input vector provided. They all use some sort of distance measure. It should be added that nonlinear neural networks and SVMs use nonlinearity to globally bend and stretch the concept of distance (neural networks are universal approximators, as proved and published by Hornik in 1989).

'Distribution-free' classifiers

ID3/C4.5 decision trees, CART, the histogram classifier, the multinomial classifier - these classifiers do not apply any distance measure. They are so-called nonparametric in their way of working. This having said, they are based on count distributions - hence the binomial distribution and the multinomial distribution, and nonparametric classifiers are governed by the statistics of these distributions. However, as the only thing that matters is whether the observed value of an input variable occurs in a specific bin/interval or not, they are by nature insensitive to extreme observations. This holds when the intervals of input variable bins to the leftmost and rightmost side are open. So these classifiers are certainly model robust.

Noise characteristics and outliers

Extreme values are one kind of noise. A scatter around a zero mean is the most common kind of noise that occurs in practice.

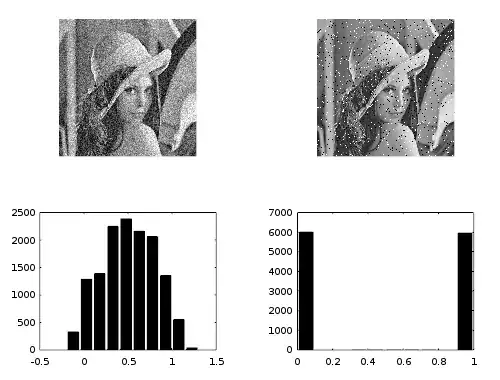
This image illustrates scatter noise (left) and salt-and-pepper noise (right). Your robustness questions relate to the right-hand kind of noise.

Analysis

We can combine the true value of classifier input $i$, $z(i)$ with scatter noise $\epsilon$, and an outlier offset $e$ as

$ x(i) = z(i) + \epsilon + e \cdot \delta(\alpha) $

with $\delta(\alpha)$ the Kronecker delta function governed by the parameter $\alpha$. The parametrized delta-function determines whether the outlier offset is being added, or not. The probability $P(\delta(\alpha)=1) \ll 1$, whereas the zero-mean scatter is always present. If for example $P(\delta(\alpha)=1) = \frac{1}{2}$, we do not speak of outliers anymore - they become common noise additive offsets. Note also that distance is intrinsic to the definition of the concept outlier. The observed class labels themselves in a training set cannot be subject to outliers, as follows from the required notion of distance.

Distance based classifiers generally use the L2-norm $\mid \mid {\bf x} \mid \mid_2$ to calculate degree of fit. This norm is well-chosen for scatter noise. When it comes to extreme values (outliers), their influence increases with the power of $2$, and of course with $P(\delta(\alpha)=1)$. As nonparametric classifiers use different criteria to select the optimal set of parameters, they are insensitive to extreme value noise like salt-and-pepper.

Again, the type of classifier determines the robustness to outliers.

Overfitting

The issue with overfitting occurs when classifiers become 'too rich' in parameters. In that situation learning triggers that all kinds of small loops around wrongly labeled cases in the training set are being made. Once the classifier is applied to a (new) test set, a poor model performance is seen. Such overgeneralization loops tend to include points pushed just across class boundaries by scatter noise $\epsilon$. It is highly unlikely that an outlier value, which has no similar neighboring points, is included in such a loop. This because of the locally rigid nature of (distance-based) classifiers - and because closely grouped points can push or pull a decision boundary, which one observation in its own cannot do.

Overfitting generally happens between classes because the decision boundaries of any given classifier become too flexible. Decision boundaries are generally drawn in more crowded parts of the input variable space - not in the vicinity of lonely outliers per se.

Having analyzed robustness for distance based and nonparametric classifiers, a relation can be made with the possibility of overfitting. Model robustness to extreme observations is expected to be better for nonparametric classifiers than for distance-based classifiers. There is a risk of overfitting because of extreme observations in distance-based classifiers, whereas that is hardly the case for (robust) nonparametric classifiers.

For distance-based classifiers, outliers will either pull or push the decision boundaries, see the discussion of noise characteristics above. Discriminant analysis, for example, is prone to non-normally distributed data - to data with extreme observations. Neural networks can just end up in saturation, close to $0$ or $1$ (for sigmoid activation functions). Also support vector machines with sigmoid functions are less sensitive to extreme values, but they still employ a (local) distance measure.

The most robust classifiers with respect to outliers are the nonparametric ones - decision trees, the histogram classifier and the multinomial classifier.

A final note on overfitting

Applying ID3 for building a decision tree will overgeneralize model building if there is no stopping criterion. The deeper subtrees from ID3 will begin fitting the training data - the fewer the observations in a subtree the higher the chance of overfitting. Restricting the parameter space prevents overgeneralization.

Overgeneralization is in distance based classifiers also prevented by restricting the parameter space, i.e. the number of hidden nodes/layers or the regularization parameter $C$ in an SVM.

Answers to your questions

So the answer to your first question is generally no. Robustness to outliers is orthogonal to whether a type of classifier is prone to overfitting. The exception to this conclusion is if an outlier lies 'lightyears' away and it completely dominates the distance function. In that really rare case, robustness will deteriorate by that extreme observation.

As to your second question. Classifiers with well-restricted parameter spaces tend to generalize better from their training set to a test set. The fraction of extreme observations in the training set determines whether the distance based classifiers be led astray during training. For non-parametric classifiers, the fraction of extreme observations can be much larger before model performance begins to decay. Hence, nonparametric classifiers are much more robust to outliers.

Also for your second question, it's the underlying assumptions of a classifier that determine whether it's sensitive to outliers - not how strongly its parameter space is regularized. It remains a power-struggle between classifier flexibility whether one lonely outlier 'lightyears away' can chiefly determine the distance function used during training. Hence, I argue a generally 'no' to your second question.

Answer 2

How does a model become "robust to outliers"? It does so by acknowledging their presence in the specification of the model, by using a noise model that contains outliers. In probabilistic modeling, this may be achieved by assuming some kind of fat-tailed noise distribution. From an optimization perspective, the same thing can be achieved by using an "outlier-robust cost function" (such as the Huber loss function). Note that there is an equivalence between these two worlds, e.g., whereas L2 norm error minimization corresponds to the assumption of Gaussian noise, L1 norm error minimization (which is more robust to outliers) corresponds to the assumption of Laplacian noise. To summarize, robustness to outliers has nothing to do with the model of the process itself; it depends only on the correctness of the noise model.

How does a model become "robust to overfitting"? Overfitting is a symptom of model mismatch: the process model is too flexible and the noise model is incorrect. If we knew exactly what level of measurement noise to expect, even a very flexible model would not overfit. In practice, robustness to overfitting is achieved by using a flexible model class but biasing the model towards simpler explanations by means of regularization (using a prior over the parameters or, equivalently, an L1/L2 regularization term).

What's the relation of the two properties? Use a flexible model class without appropriate parameter priors or regularization and assume a fat-tailed noise distribution or a robust loss function, and you have an inference procedure that is robust to outliers but not to overfitting. Use an appropriate regularization term but usual L2 error minimization, and you have a method that is robust to overfitting but not to outliers. The two properties are orthogonal to each other, since they relate to different components of the assumed statistical model: robustness to outliers depends on the correctness of the noise model / error loss function, whereas robustness to overfitting depends on the correctness of the parameter priors / regularization term.

Answer 3

There is a lot of things to influence the outliers, if the model is overfitting then it will learn specific details of data including noise data points like outliers. But it's not necessarily that if model not robust to outliers then it's overfitting, there is models is sensitive to outliers.

Answer 4

Per Wikipedia on contraposition to quote:

In logic and mathematics, contraposition refers to the inference of going from a conditional statement into its logically equivalent contrapositive, and an associated proof method known as proof by contraposition.[1] The contrapositive of a statement has its antecedent and consequent inverted and flipped. For instance, the contrapositive of the conditional statement "If it is raining, then I wear my coat" is the statement "If I don't wear my coat, then it isn't raining."...The law of contraposition says that a conditional statement is true if, and only if, its contrapositive is true.[3]

So, on the slightly reworded question: Is a model that does not overfit easily than one that does, necessarily implied more robustness to outliers, the contraposition is, as 'not more' is 'equal or less': Does equal or less robustness necessarily follow from a model that overfits easily than one that does not?

To assist in the answer, take the case of Least Absolute Deviation regression which is known for its robustness. It also curious in the case of estimation of single parameter, it reduces to a median estimate as opposed to the mean (which is highly susceptible to outliers as it incorporates all the data). So, the mean can be viewed as 'overfitting' but in samples, the mean and median can be close due to a balancing of large positives and negative values.

Per the 'if and only if standard' placed on the veracity of the councontrapositive, necessarily less robustness does not follow from a model that overfits easily than one that does not, so my answer is no.