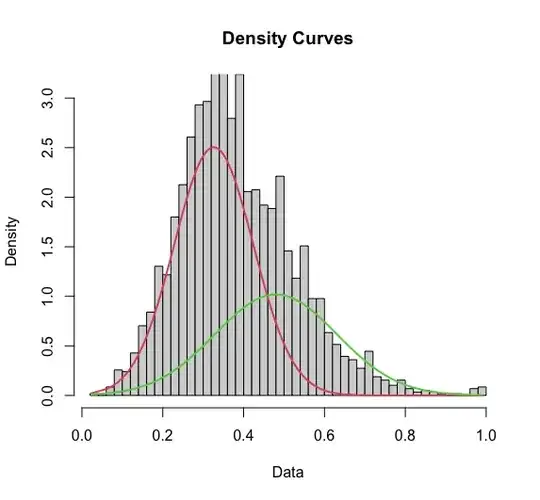
I've modeled my data with a mixture model of two gaussians centered at approximately 0.33 and 0.5, respectively.
Now I want to "assign" a probability to each data point that it belongs to either of the distributions.
I've tried implementing the following approaches:
First, I estimate the likelihood of each data point under each curve:
likelihood_0.33=dnorm(ith_data_pt,mean=mu[1],sd=rsigma[1])*lambda[1]
likelihood_0.5=dnorm(ith_data_pt,mean=mu[2],sd=sigma[2])*lambda[2]
... and assign each point to the distribution for which it has a greater likelihood.
Alternatively, I estimate probability that a data point came from a given distribution:
if(ith_data_pt>mu[1]) {
prob_0.33=pnorm(ith_data_pt,mean=mu[1],sd=sigma[1],lower.tail=F)
}
else {
prob_0.33=pnorm(ith_data_pt,mean=mu[1],sd=sigma[1])
}
if(ith_data_pt>mu[2]) {
prob_0.33=pnorm(ith_data_pt,mean=mu[2],sd=sigma[2],lower.tail=F)
}
else {
prob_0.33=pnorm(ith_data_pt,mean=mu[2],sd=sigma[2])
}
Using the "likelihood" approach, I get the following "spread" for my population assignments:
0.3 0.5
1626 1290
...While using the "probability" approach, I get:
0.3 0.5
2099 817
Which of these two methods is a more valid means of assigning "membership"? Why?
Thanks in advance!