3

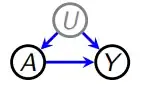
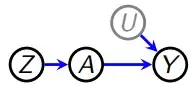
Someone suggested the following idea to me to control for reverse causality. Suppose we want to test for the effect of $X$ on $Y$ in a panel data set, but we suspect that there is reverse causality. That is, past values of $Y$ may cause variation in $X$, too.

The suggestion goes as follows: In order to remove potential reverse causality between independent variable $X_t$ and dependent variable $Y_t$, we could run a first stage regression of the second lag of $y$ on the first lag of $x$,

$$x_{t-1}=\alpha + \beta y_{t-2} + e_{t-1}$$

and then use the residuals of that regression $e_{t-1}$ as the independent variable in our main model

$$y_t = \beta_0 + e_{t-1} + z_{t-1}$$

Here, $e_{t-1}$ would thus represent the part of $x_{t-1}$ that is not explained by preceding values of $y$. This method should therefore effectively remove the reverse causality in the model.

The proposition makes intuitive sense to me at least. However, I have not seen it proposed or applied anywhere before, the common remedy for reverse causality being 1) lagging independent variables, and b) using IVs. Though I admit that I am perhaps not skilled enough an econometrician to give an adequate response here. I was therefore hoping the community could weigh in on the question. Does this method seem viable to you as a control for reverse causality, or have you seen it (or something similar) applied somewhere before?

altabq
  • 665
  • 3
  • 6
  • 16

1 Answers1

1

The approach seems to be correct although the expression for $x_{t-1}$ and $y_t$ may not be. Ths is an instrument variable model where the causality between X and Y needs to be inferred in the presence of a confounder affecting both. Consider a DAG confounding variable where we want to understand the effect of A on X. Because there is an unknown/unobserved variable U affecting both A and Y, we cannot have the independence between Y(a) and A. Y(a) is the random variable when A is fixed to some value a. Now, imagine there is another variable Z that can completely predict A and hence renders the arrow connecting U->A completely useless i.e, Z is an instrument variable. Due to this strong predictor of A, we can have $Y(a) \perp A$. In most cases however, you are going to have a middle ground between the two which implies $Y(a,z) \perp {A}$. It allows us to create linear models to understand the causal relationship between A and Y.

  1. $A = v_0 + v_1 * Z + e_1$
  2. $Y = u_0 + u_1 * A + e_2$ and,
  3. $Y = w_0 + w_1*Z + e_3 $

Getting the average causal effect of A on Y i.e, $E[Y(1)] - E[Y(0)]$ is now straight forward. Using Sewell path analysis method gives us $E[Y(1)] - E[Y(0)] = \frac{E[Y(z=1)] - E[Y(z=0)]}{E[A(z=0)] - E[A(z=1)]} = \frac{w_1}{v_1}$

$Y_{t-1}$ is doing the same job as Z in your case

prayingMantis
  • 11
  • 1