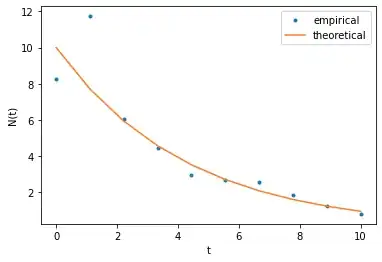
I am trying to fit a curve to empirical data where I know that uncertainty is in the predictors ($X$) (there could be also an uncertainty in $Y$, but let's keep things simple for the start). In other words, I know only the expected values, but not the true values of $X$.
My model is somewhat complicated, but I'll try to use a simplification as an example. Say I want to determine the rate of the decay b of a compound. Based on my domain knowledge I assume the following model:
$$ N_t = N \cdot e^{-bt} $$
I set up the experiment in which I start with theoretically always the same amount N0 of the compound, wait some pre-defined time t0, which I vary over the repeated runs of the experiment, and measure the actual remaining amount Nt of the compound. However, I have errors both in N0 and in t0, so that the actual (but unobserved!) starting amount N and the waiting time t are random variables, say, normally distributed around N0 and t0, respectively.
In code:
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1)
b = .2345
N0 = 10
N = N0 + np.random.randn(10)
t0 = np.linspace(0, 10, 10)
t = t0 + np.random.randn(10)
Nt = N * np.exp(-b * t)
plt.plot(t0, Nt, '.', label='empirical')
plt.plot(t0, N0 * np.exp(-b * t0), label='theoretical')
plt.legend(loc='upper right')
plt.gca().set_xlabel("t")
plt.gca().set_ylabel("N(t)")
How would I determine b in a maximum likelihood manner?
I have read Simple linear regression model with random x, Regression with random X, Find P(Y=y | X=x) when X is a continuous random variable, and What are the Differences in Linear Regression of Y vs X when both Y,X are Random and Regressing Y vs X when X is Mathematical, but they don't seem to answer my specific question (or in an abstract way which I was unable to comprehend).