Coin throws are most probably modeled as binomial random variables. If I throw the coin $2n$ times, then the probability I get exactly $n$ heads and $n$ tails would be
$$ P(x = n) = {2n \choose n} p^{n}(1-p)^{n} $$
Assuming the coin is fair, we get
$$ P(x = n)={2n \choose n} \dfrac{1}{2^{2n}} $$
which very quickly becomes 0. That's because there are more ways to NOT get 50/50 tosses than ways to get 50/50 tosses. You can easily plot this using any software of your choice or just compute it for a given number of throws.
As to your second question, jt would be better to talk about the probability of being within some range of 50/50 rather than asking for a number which would guarantee you achieve this precision. In the limit, the sampling distribution for the sample proportion looks like
$$ \hat{p} \sim \mathcal{N} \left( p, \dfrac{p(1-p)}{n} \right) $$
The probability that the sample proportion is within $d$ of 0.5 is
$$ P( \vert \hat{p} - 0.5 \vert < d ) = P(-d+0.5 < \hat{p}< d+0.5) $$
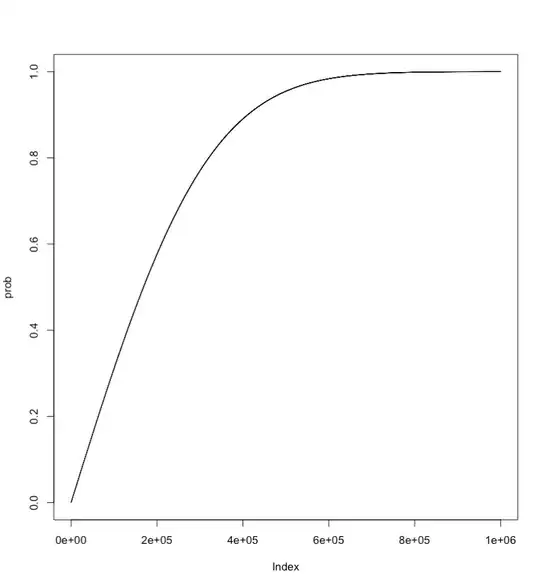
I'm sure this could be simplified further in terms of CDFs and then inverted with some clever algebraic approximation so that you get flips as a function of probabilities, but frankly its Sunday and I'll let someone else do that. Because we are using a normal as our approximation, this is quite easily computed as a function of $n$.
d = 1e-6
prob = pnorm(d+0.5, 0.5, 0.25/1:1e6) - pnorm(-d+0.5, 0.5, 0.25/1:1e6)
plot(prob, type = 'l')