Have I presented this Mann-Whitney U test appropriately?

Question

I have collected data from two populations, M (males) and F (females) through a Likert scale of their agreement to a statement X

The data is the following for females F

And for M males

As you can see it is from strongly disagree to strongly agree. For analysis this was converted to a scale from 1 to 5 and a Mann-Whitney U test was done to compare the distribution of both populations' answers.

1. Could you tell me whether I have explained this adequately in the 'analysis' part of my paper and if I have reported the results in an appropriate format? Also is using the mean (+/- SD) OK for comparing the two groups' distribution qualitatively as I have done?

Analysis: "Likert-scale data was treated as ordinal (1-5) and subsequently analysed using the Mann-Whitney U-test when appropriate"

Results: "There was no significant difference between females’ opinion (mean Likert score: 3.06 ± 1.095) and males’ opinion (mean Likert score: 3.00 ± 1.113 ) of the importance of being asked x (U = 5813, z = 0.587, p = .5552)."

2. Are the results correct? I haven't used any stats software, just an online calculator (as I have no skills in R or even SPSS). Is anyone able to check?

Answer 1

As for the check with SPSS or R, suitable R code could be the following. Unfortunately I can only tell you a way via Wilcoxon W, not Mann-Whitney U. The tests are equivalent, though:

library(exactRankTests)
f <- c(rep(1,21), rep(2,17), rep(3, 82), rep(4,34), rep(5,18))
m <- c(rep(1,7), rep(2,15), rep(3,28), rep(4,13), rep(5,8))
wilcox.exact(f, m)

The result would be

> wilcox.exact(f, m)

    Asymptotic Wilcoxon rank sum test

data:  f and m
W = 6399, p-value = 0.5343
alternative hypothesis: true mu is not equal to 0

Where you could cite R in the literature as

R Core Team (2020). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.

and the package exactRankTests as

Torsten Hothorn and Kurt Hornik (2019). exactRankTests: Exact Distributions for Rank and Permutation Tests. R package version 0.8-31. https://CRAN.R-project.org/package=exactRankTests

As for the rest of the description, that depends a lot on personal taste, faculty etc. I for one would be careful to call something that has been measured by only one Likert-type item as a Likert scale. Also you seem to use Likert scale data and Likert score somewhat identical. Why two different words then? Apparently, you have interviewed 243 persons. Does it seem appropriate to use that many digits for standard deviation and p-value?

So the calculation is about right, detail in the wording has to do with personal taste.

Answer 2

I have no disagreement with @Bernhard's Answer (+1), but I will give my own comments on this using R, especially because you have not up-voted or accepted the answer, and you still seem puzzled in some of your comments.

The Likert scores and summaries are as follows:

wom = rep(1:5, c(21,17,92,34,18))

summary(wom)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   1.00    3.00    3.00    3.06    4.00    5.00 

men = rep(1:5, c(7,15,28,15,8))

summary(men)       
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.000   2.000   3.000   3.027   4.000   5.000 

The two sample medians are 3.0, so I think it is better just to say that, than to try to give confidence intervals. Giving confidence intervals for means seems undesirable because

• The methods for making those confidence intervals seem to be based on an assumption that data are from a continuous normal distribution, while they are actually ordinal categorical data.

• Also, I agree with the objection that CIs for means (besides being pointless) might confuse your readers, making them wonder what those CIs have to do with your nonparametric test (which is nothing at all).

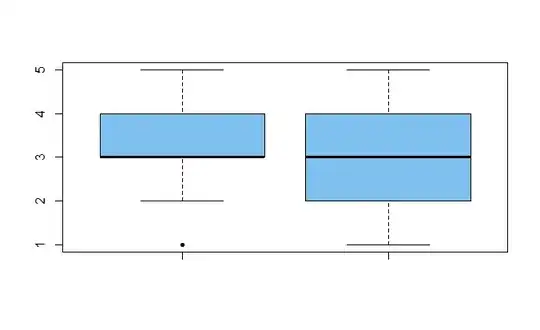
Boxplots leave little doubt that the medians for men and women are both $3.$

boxplot(men, wom, col="skyblue2", pch=20)

I agree that a 2-sample Wilcoxon rank sum test does not find a difference between the two samples of Likert scores.

wilcox.test(men, wom)

        Wilcoxon rank sum test 
      with continuity correction

data:  men and wom
W = 6829, p-value = 0.711
alternative hypothesis: 
  true location shift is not equal to 0

Data summaries and box plots seem to show a few more low (disagree) scores among women than among men. However, a chi-squared test of homogeneity of Likert scores for men and women does not reject the null hypothesis of homogeneity.

TAB = rbind(c(21,17,92,34,18),
            c( 7,15,28,15, 8))
TAB
     [,1] [,2] [,3] [,4] [,5]
[1,]   21   17   92   34   18
[2,]    7   15   28   15    8

chisq.test(TAB)

        Pearson's Chi-squared test

data:  TAB
X-squared = 7.1942, df = 4, p-value = 0.126

I think it may be sufficient to say that both Men and Women have median 3 Likert scores and that a Wilcoxon rank sum test (equivalent to Mann-Whitney) finds no significant difference in locations, with P-value 0.71. If you feel you need to say more, then perhaps mention the P-value 0.13 for the chi-squared test of homogeneity.

Finally, I think it is worth mention somewhere the exact numbers of men and of women in the study (and if not obvious from the context, the reason for such different numbers).

Answer 3

This is partly a comment on @Bruce ET's helpful answer, but the graph here won't fit in a comment -- and inviting or expecting readers to enter the data and draw it for themselves is unrealistic.

The box plot isn't wrong, as box plots go, and makes the point that the medians are the same for males and females. But box plot conventions make the display overstate the difference between males and females in distribution.

Also, the box plot does precisely what is implied to be wrong about calculating means, treat the grades or ratings Strongly agree to Strongly disagree as equally spaced points on a measured scale, here 1 2 3 4 5. This is important because the box plot display hinges on calculation of median and quartiles and (specifically here) uses 1.5 IQR in deciding where whiskers stop and whether data points are shown beyond the ends of whiskers.

Indeed, experience on Cross Validated and elsewhere shows that box plots for graded or ordinal data like these -- more generally, for data with many ties -- are often puzzling. They can even provoke suspicions that something is wrong. (Usually the software is put in question, not the reader of the graph.) These example threads understate the puzzlement box plots can cause.

Boxplot interpretation: is it correct that a boxplot is missing a whisker?

Help needed with my box plot

A plain bar chart explains why and how the box plot muddies the picture. Bar lengths here are proportional to percents given gender, but the annotation shows absolute counts too. Indeed, my bar chart also shows grades equally spaced, but nothing depends on that conventional spacing.

For males, the distribution is such that median and lower quartile agree at 3. So, the interquartile range is just 1: this is clear from the graph, as it is the height of the box. So, the lowest value 1 qualifies for separate display: it is 2 below the lower quartile, and so more than 1.5 IQR away from the lower quartile, which is the most common convention for separate display of low values and that used by R in this case. (I don't join the poor practice of shouting "outlier" here.)

For females small differences between the distributions make the lower quartile emerge as 2, and the lowest value 1 is not selected for separate display.

The box plot does not, and cannot, tell you much about the relative frequency of grades of 1, which are not much different for males and females, or about the relative frequency of any other grade for that matter.

Answer 4

I would say that your presentation of the Mann-Whitney U test is slightly sloppy, although in practice it hardly matters. Intuitively, you are in the right direction, but it wouldn't hurt to be more correct.

Mixing of concepts

"There was no significant difference between females’ opinion (mean Likert score: 3.06 ± 1.095) and males’ opinion (mean Likert score: 3.00 ± 1.113 ) of the importance of being asked x (U = 5813, z = 0.587, p = .5552)."

This sentence might be confusing because it is combining three concepts. It is talking about:

• General differences between distributions:

  "There was no significant difference between females’ opinion ... and males’ opinion"

  For this, if you just want to test whether there are any differences, you might better use a chi-squared test.

• Means of distributions and their error estimates:

  (mean Likert score: 3.06 ± 1.095) ... (mean Likert score: 3.00 ± 1.113 )

  You write scores with confidence intervals or with expressions for the error. For these types of statistics, to compare significance, one would expect something like a t-statistic, instead of a U-statistic.

• A U-statistic:

  (U = 5813, z = 0.587, p = .5552)

  The U-statistic (and related z-score) is a test for equivalence of distributions, but it is only sensitive to a specific type of alternative hypothesis. The Mann-Whitney test is only sensitive for the alternative P(X>Y). A chi-squared test relates to all possible differences between the distributions and might be more intuitive when you wish to express whether the opinions differ.

  Use the Mann Whitney test when you wish to specifically test the idea that one variable is larger (higher order) than the other (personally I would not do this when you only have 5 categories and variations might be occurring in more than just differences in order).

---

Why Mann-Whitney test is not presented appropriately

• One aspect is that the Mann-Whitney U test is not a test for differences between means.

  This, Mann-Whitney U test is used to test differences in means, is a bit implied when you mix those three concepts (described above) in the same sentence.

  The Mann-Whitney U test relates to the question of stochastic dominance $P(X>Y) \neq 0.5$ and not to the question of different means.

  On the one hand you can have different means but no stochastic dominance. On the other hand you can have stochastic dominance but not different means. They are different things.

  In practice they may coincide: for instance, if you envision the same distribution with only a shift in the location then you get that the difference in means will coincide with a difference in stochastic dominance. But in your case I would not use that assumption with 5 points.

• You are comparing the means of a Likert scale by converting the categories into a scalar number. This might seem right since both the 'Likert scale' and the 'number system/scale' have an order. However, something that is not equal between them is a concept of scale or distance.

  This does not mean that you can not compare the means. The resulting 'mean' of that scale is a number which you can compare for different groups. However, you need to be careful in the interpretation (the same would be true if you are dealing with actual scalars).

  Comparing means becomes tricky when distributions differentiate on more aspects than just a shift in the mean. If the distributions are different in more ways than just a shift then the differences in the mean are dependent on the scale.

  The difference in the mean will not be invariant for a change in the scale.

  For instance take your distributions:

            SD    D     N     A     SA
   men      7     15    28    13    8
   women    21    17    82    34    18
  

  If you assign the values $1,2,3,4,5$ to those categories then you will get averages $$3.064 = \bar{X}_{women} > \bar{X}_{men} = 3.000$$ but if you assign values $e^2,e^4,e^6,e^8,e^{10}$ to the categories (or anything else that increases the weight of the fifth category) then $$3092 = \bar{X}_{women} < \bar{X}_{men} = 3199$$

---

About the Mann-Whitney U test

Intuitively you can consider the Mann-Whitney U test as comparing something like an empirical joint distribution (the numbers in the cells are the product of the numbers in the margins, e.g. the upper left number $147 = 7 \times 21$):

$$\begin{array}{cc | cccccccc} &&\text{SD} &\text{D}&\text{N}&\text{A}&\text{SA}\\ & &7 & 15& 28 & 13 & 8\\ \hline \text{SD}&21& \color{gray}{147} & \color{blue}{315} & \color{blue}{588} & \color{blue}{273} & \color{blue}{168}\\ \text{D}&17& \color{red}{119} & \color{gray}{255} & \color{blue}{476} & \color{blue}{221} & \color{blue}{136} \\ \text{N}&82& \color{red}{547} & \color{red}{1230} & \color{gray}{2296} & \color{blue}{1066} & \color{blue}{656}\\ \text{A}&34& \color{red}{238} & \color{red}{510} & \color{red}{952} & \color{gray}{442} & \color{blue}{272} \\ \text{SA}&18 & \color{red}{126} & \color{red}{270}& \color{red}{504} & \color{red}{234} &\color{gray}{144} \\ \end{array}$$

And the question is: Do I get more observations in the upper right corner (men more often higher than women, blue) or in the lower left corner (women more often higher than men, red)?

This table relates to the probability that two random men and women from your sample will be equal (gray) or different, men>women (blue) or men<women (red).

You get the following score if you compare how often the men's score is higher than the women's. $$\color{blue}{315+588+273+168+476+221+136+1066+656+272}+\frac{1}{2}\color{gray}{(147+255+2296+442+144)} = 5813$$

You get the following score if you compare how often the women score higher than the men. $$\color{red}{119+574+1230+238+510+952+126+270+504+234}+\frac{1}{2}\color{gray}{(147+255+2296+442+144)} = 6399$$

The distribution of these scores can be imagined by considering randomly ordering the two categories. This is what Mann and Whitney did and they showed that the distribution of the U score is approximately a normal distribution.

Graphical representation

It may help to plot the percentages of the results.

You can see that for women and men you have more or less similar frequencies in the 'strongly disagree' and in the 'agree' and 'strongly agree' categories. It is in the categories 'disagree' and 'neutral' that you see that men are relatively more often in the disagree category and less often in the neutral category (or from the other perspective women less often in the disagree category and more often in the neutral category).

These differences are not very large. We can also see this based on a chi-squared test for the equivalence of the two distributions ($\chi^2 = 5.9037, df = 4, p = 0.2065$). But it might be interesting for further investigation to see whether men are often less nuanced (less often 'N') in comparison to women, and in place of that more often slightly negative (more often 'D').