5

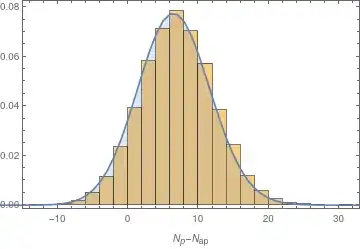
I have a data set with counts of particles, and I want to test if they follow a distribution. For a certain species, I make the $\chi^2$-test, and everything seems reasonable, finding a $p$-value of $p=0.75$, which I interpret as meaning that my null hypothesis (in this case, that the data follows a Skellam distribution) is not rejected. In the plot below, the histogram is the binned data and the curve is the expected distribution.

p-ap

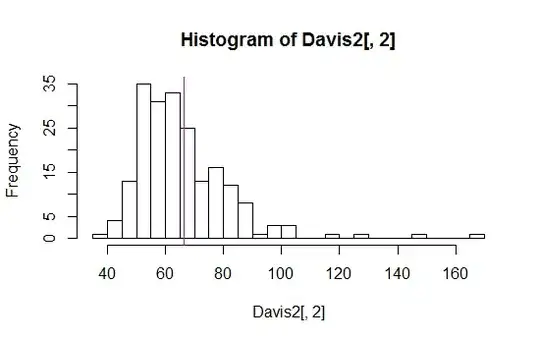
However, when I do the same for another type of particle, I find the $p$-value of $p=2\times 10^{-13}$, but the plot suggests to me that the data does follow the Skellam distribution:

pi+-pi-

I read in some places that a large sample may cause this, but my sample size is $3\times10^4$, and as it didn't affect the first type of particles, I'm assuming that is not the problem. What am I misunderstanding here? Does it really mean that I should reject the null hypothesis?

A follow-up question: which test should I use to check the goodness-of-fit, in this case? For completeness, the statistic is $\chi^2=19.8$ and $\chi^2=220$, respectively.

COOLSerdash
  • 25,317
  • 8
  • 73
  • 123
Renan Nobuyuki Hirayama
  • 181
  • 6
  • 3
    Related but specific to normal distributions: https://stats.stackexchange.com/questions/2492/is-normality-testing-essentially-useless?noredirect=1&lq=1 – Dave Jun 10 '20 at 20:51
  • 4
    3 x 10^5 is a very large sample in most contexts. – Bryan Krause Jun 10 '20 at 20:54
  • Low p-values are indicators for anomalies. But you shouldn't forget that the test to which the p-value relates entails the *entire* experiment. It can be that your hypothesis is wrong, it can also be that your experiment is wrong. The p-value is just testing an idealistic probability distribution, and it does not include the fluctuations in measurements that may occur due to systematic errors (e.g. think of the "discovery" of superluminal neutrinos). – Sextus Empiricus Jun 10 '20 at 21:47
  • If you have a large sample size then you can significantly measure tiny fluctuations. – Sextus Empiricus Jun 10 '20 at 21:50
  • @SextusEmpiricus, I understand, but these are simulated events, so I don't think that's the case – Renan Nobuyuki Hirayama Jun 10 '20 at 21:51
  • Could you provide a table of your data based on which you did the chi-squared test. Possibly your plots are not accurate (I find the apparent shift of the curve in the first plot strange). – Sextus Empiricus Jun 10 '20 at 21:52
  • 3
    @RenanNobuyukiHirayama these are SIMULATED events? So you can guarantee that the null hypothesis is actually true (assuming you haven't got a bug in your code)? – Hong Ooi Jun 11 '20 at 04:56
  • As others said, low p values for seemingly small effects can be due to large samples (and 3000 is large in this context). But, rather than a density plot and histogram, you could look at a QQ plot to get a better idea of any deviations. – Peter Flom Jun 11 '20 at 12:32
  • @HongOoi, I'm actually trying to check if the hypothesis is true for different decay configurations on a freeze-out (this data is only one configuration, but the low $p$-value is common to all of them). In non-physics terms, I'm checking that a certain process doesn't introduce correlations between particles, which has the consequence of making the net-X be Skellam-distributed, and I can't check it directly from the code (which I also hopefully assume has no bugs). – Renan Nobuyuki Hirayama Jun 11 '20 at 14:03

1 Answers1

8

A few general thoughts:

  1. It's very rare that real-world data follow a specific distribution exactly. This doesn't stop us from using a specific distribution as a model in order to answer questions. A model doesn't have to be perfect, but good enough for the purpose.
  2. With such a huge sample size, even tiny deviations from a Skellam distribution will result in very small p-values. This is just a result of the consistency of the tests. The power to detect smaller and smaller deviations increases with increasing sample size (see also here). In the second case, a p-value of $2\times 10^{-13}$ means that there is a lot of evidence against the null hypothesis that the data come from a Skellam distribution. Specifically, there are $-\log_{2}(2\times 10^{-13})\approx 42.19$ bits of information agains the test hypothesis (this is called the $S$-value).
  3. A failure to reject the null hypothesis does not mean that it is true. It means that there is not enough evidence to reject the notion that your data are compatible with a Skellam distribution with a high enough confidence. There may be infinitely many distributions other than the Skellam distribution that are compatible with your data.
  4. Histograms are suboptimal to check the agreement between the data and a specified distribution. I recommend to use Q-Q-plots instead (more information here). Another very useful visualization tool is the hanging rootogram. A good paper on this can be found here. I show how to apply a hanging rootogram to check the fit to a Poisson distribution in this answer.

In the light of the points above, here are some questions that you might find useful to ask yourself:

  1. What's your specific goal? Why do you want to show that the data are following a Skellam distribution?
  2. How large do the deviations from a Skellam distribution have to be in order for you to deem the model of a Skellam distribution unsuitable for the task?

Both of these questions require subject matter knowledge which I don't have.

COOLSerdash
  • 25,317
  • 8
  • 73
  • 123
  • 1
    Though general, these thoughts clarified some misconceptions I had (Thanks!). A follow-up question that doesn't seem to deserve its own post: Which test to check the goodness-of-fit should I use? And to answer your questions: 1. This data is the net-proton (proton minus antiprotons) and net-pion ($\pi^+ - \pi^-$) number after a heavy-ion collision, which should be Skellam-distributed if the particles are emitted independently. 2. I'm not sure, at least yet. – Renan Nobuyuki Hirayama Jun 10 '20 at 21:10
  • @RenanNobuyukiHirayama A $\chi^{2}$-test seems fine to me but I don't have a lot of experience regarding goodness-of-fit tests. I hope someone more knowledgable can make a more informed recommendation. – COOLSerdash Jun 10 '20 at 21:16
  • 2
    excellent answer! @RenanNobuyukiHirayama chi square test is very appropriate, you may favour g-test, which is a bit more solid in its convergence, but it's almost the same thing. Since Skellam distribution is almost gaussian, another good option could be Anderson-Darling, which is not specifical for gaussianity, but known to perform well in that case. – carlo Jun 10 '20 at 22:27
  • I should add that AD test is fairly different from chi square test, but most of the times they give the same result, as they test the same hypothesis. – carlo Jun 10 '20 at 22:39
  • 1
    For reference, I made the suggested QQ plot, posted it here: https://imgur.com/a/6SzmPmX The Skellam distribution agrees with the data very well, but I'm still curious about a quantification of this agreement (something like reduced residuals) – Renan Nobuyuki Hirayama Jun 11 '20 at 16:04