You don't need hacks, this can be tackled using vanilla Bayes theorem. The more informative your prior is, the more weight in has on the final result. The opposite is also true, the more information your data provides, so also the larger sample size, the more weight it has. So just have your priors to be more informative. To achieve this, you need priors that concentrate more probability mass over the outcomes you assumed to be most likely a priori, e.g. decrease variance of normal prior distribution. Stronger prior would need much more evidence to be "convinced" by the data, so your "untrustworthy" data would need to be very strong. If your data overcomes the strong, informative prior, maybe it’s not that bad after all?
Below you can find an example of beta-binomial model, where for the same data, and same model, we use priors that are centred on same mean for $p$, but differ in how informative they are (from least, to most). As you can see, the more informative the prior, the more influence it has on posterior (the closer it ends to prior).
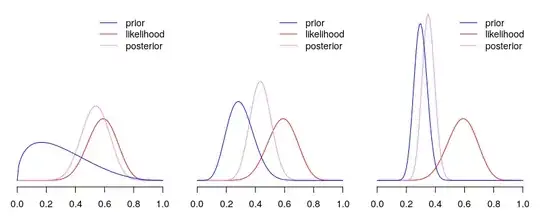
Disclaimer: if you try reproducing plots as above, notice that I re-scaled likelihood, so that it roughly matches the scale of prior and posterior. This does not matter for the results, but makes the plots more readable.
With introducing a weight for prior, as you did in your question, or data, as suggested in comments and other answer, you'd introduce additional hyperparameter that needs to be tuned. Moreover, this would make interpretability of the results harder, since the impact of the prior would get much less trackable. With vanilla Bayes theorem, there is no such problem, where the quantities that go into equation are well-defined and the outcome is a proper probability.
It is also worth asking yourself why do you consider this data as "untrustworthy"? I assumed in here that what you meant is that is is "noisy", so you want to catch up by forcing some assumptions by the priors. Another case is that the data is simply wrong, but then why would you use it at all? If you would need to hack your model to ignore the data, then this isn't statistics anymore. Another case is if the uncertainties are known for the datapoints, then you can always use sample weights, or error-in-variable model.
