I have two independent random variables which follow binomial distributions $X \sim B (n_1, p_1)$ and $Y \sim B (n_2, p_2)$.
Can we say that $Z = X + Y$ is also binomially distributed $Z \sim B (n_1+n_2, (p_1+p_2)/2)$? Can you explain the answer to me please?
I have read many articles without finding the answer. I know that if $p = p_1 = p_2$ then we can say that $Z \sim B (n_1+n_2, p)$. But what can we say when $p_1\neq p_2$?
Comments:
(a) Let $X \sim \mathsf{Binom}(10,.2),$ $Y \sim \mathsf{Binom}(10,.8),$ and $W \sim \mathsf{Binom}(20,.5).$ Then $Var(X) = Var(Y) = 1.6$ and $Var(X+Y)=3.2.$ But $Var(W) = 5.$ So $X+Y$ and $W$ can't have the same distribution.
(b) $P(X+Y = 0) = P(X=0,Y=0) = P(X=0)P(Y=0) \ne P(W = 0).$
pbinom(0,10,.2)*pbinom(0,10,.8)
[1] 1.099512e-08
pbinom(0,20,.5)
[1] 9.536743e-07
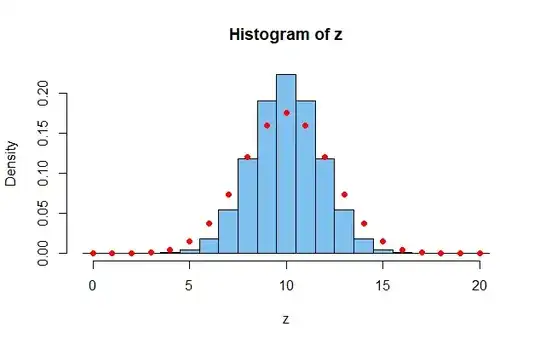
(c) For $X \sim \mathsf{Binom}(10,.2)$ and $Y \sim \mathsf{Binom}(10,.8),$ here is R code to make a histogram of a large sample from $Z = X + Y.$ Then the red dots show the distribution $\mathsf{Binom}(20, .5).$ The dots don't match the histogram.
set.seed(1234)
m = 10^6
x = rbinom(m, 10, .2)
y = rbinom(m, 10, .8)
z = x + y
mean(x); var(x)
[1] 2.000237 # aprx E(X) = 2
[1] 1.603947 # aprx Var(X) = 1.6
mean(z); var(z)
[1] 10.00093 # aprx E(Z) = E(X) + E(Y) = 2 + 8 = 10
[1] 3.208881 # aprx Var(Z) = Var(X)+Var(Y) = 1.6+1.6 = 3.2
cutp = (-1:20)+.5
hist(z, prob=T, br=cutp, col="skyblue2")
k = 0:20; pdf=dbinom(k,20,.5)
points(k,pdf, col="red", pch=19)
