0

English Wiki states that Sturges' formula is $$k = \lceil log_2(n) + 1 \rceil$$ whereas, for example, Russian Wiki postulates it as $$k = \lfloor log_2(n) + 1 \rfloor.$$ Other sources mention rounding to the nearest integer, and the original paper does not compute $k$ at all, instead calculating class interval, later rounded to convenient multiplies of 2 and 5, which I guess was compensating for the lack of computers at that time.

So what is the difference between rounding logarithm down and up?

theuses
  • 109
  • 1
  • If you have a particular distribution in mind, generate its random deviates, and see if you can construct an improved rule based on examining repeated simulation runs. – AJKOER Jun 06 '20 at 19:52
  • 2
    Since all such formulas are rules of thumb to establish an initial number of bins *as a point of departure for creating a better histogram,* why would the rounding matter?? – whuber Jun 06 '20 at 20:07
  • @whuber consider a chi squared test given some data from supposedly normal distribution. First we need to group data into k bins, and changing k might change value of statistic. – theuses Jun 06 '20 at 20:29
  • That's a good point. In response, let me observe (1) if you do the grouping based on what you see in the data, the chi-squared test may be invalid; (2) if the decision is sensitive to the grouping, the results are going to be suspect unless every part of the data collection and analysis is conducted with utmost rigor. See the discussion of the chi-squared test in my post at https://stats.stackexchange.com/a/17148/919. – whuber Jun 07 '20 at 14:05

1 Answers1

1

Several frequently used rules. Sturges' Rule is only one of several the histogram binning rules in common use. Two other rules in common use include 'Freedman-Diaconis' and 'square root'. The choice of the number of bins depends on the type of data to be illustrated, the purpose of the histogram, and the audience who will interpret it. No rule is adequate for all situations.

The quest for 'convenient' bin boundaries did not disappear with the computer age. All software I have used seeks 'round number', equally-spaced boundaries.

Histogram binning in practice. For example, using basic graphics in R, hist, allows one to 'suggest' a number of bins, overriding the default formula, but R still choses boundaries authors of the procedure suppose are convenient. As explained in the documentation for 'hist', parameter br also accepts codes for various methods.

One can also supply a 'mandatory' list of bin boundaries, but if bins are not of equal width, a density histogram is used so that the vertical axis makes sense. (Absent a compelling reason, I think it is a bad idea to specify unequal bin widths.)

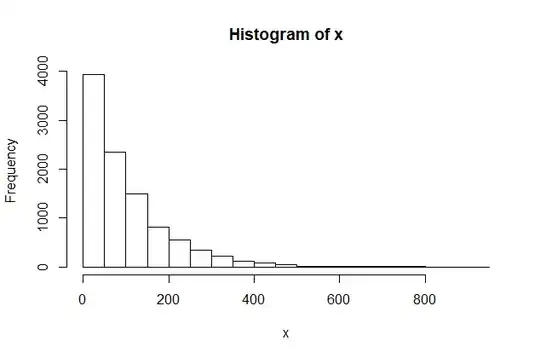
Several histograms for the same dataset. We use a sample of size $n=10\,000$ from $\mathsf{Exp}(\mathrm{rate} = 1/100).$ Here are a few examples of histograms in R--out of very many that might have been given:

In hist the default method of determining the number of bins is Sturgis' rule which suggests about 14 bins. R uses a few more to make 'nice' boundaries. (I think some of your concerns about details of using Strugis' rule become moot in practical applications.)

log2(10000)
[1] 13.28771

set.seed(606)
x = rexp(10000, .01)
hist(x)

enter image description here

By contrast, the Freedman-Diaconis rule suggests between 85 and 90 bins. As I understand it, one purpose of this rule is to give a good view of the density of the population from which the sample was sampled, so the density function of $\mathsf{Exp}(\mathrm{rate}=0.01)$ is superimposed on this histogram.

h = 2*IQR(x)/length(x)^(1/3)  # width of bars
k = diff(range(x))/h;  k      # number of bars
[1] 88.65872

hist(x, prob=T, br="FD")
  curve(dexp(x, .01), add=T, col="blue", n=10001)

enter image description here

If I want to make room for frequency labels, then I need fewer, wider bars.

hist(x, br=8, ylim=c(0,7000), label=T)

enter image description here

If I want roughly the same number of observations in each interval, I need unequal bin widths for these data. Then the vertical scale must be 'Density', and the density of my last interval would need to be expressed to five places. A clear purpose and careful planning are necessary to get a useful result for a histogram with unequal bin widths.

cutpt = c(0,100,200,400,1000)
hist(x, br=cutpt, ylim=c(0,.007), label=T)

mean(x > 400)/(1000-400)
[1] 3.033333e-05   # That is, 0.00003

enter image description here

BruceET
  • 47,896
  • 2
  • 28
  • 76
  • Forgot to mention that data is drawn from approximately normal distribution, so Sturges' rule seems a reasonable choice, but your comparison of binning in one particular PL doesn't answer question at all. I'm interested in semantics behind choosing $n$ and $n+1$ for specific formulae – theuses Jun 06 '20 at 22:11
  • 1
    OK then, English and Russian Wikipedia do give slightly different answers. One uses the 'ceiling' (round up) function and one uses the 'floor' (round down) function. [This will certainly not be the only disagreement between two versions of a Wikipedia article.] But it **absolutely doesn't matter** because, in practice, Sturgis' and other rules are only approximate suggestions how many bins to use. I attempted to illustrate this in my Answer. I'm sorry you feel it "doesn't answer your question at all!" [We try to frame answers to questions so they are of general interest.] – BruceET Jun 06 '20 at 22:23