I'm evaluating a classifier performance on a hold out test set, using AUC (and other metrics).
I'm using bootstraps to calculate the confidence intervals of the metrics.
How should I calculate if there is a sigficance difference between two classifiers?
I was going to compare the two distributions (calculated independently). But I'm beginning to think I should calculate the distribution of the differences calculated using the same bootstrap sample for each classifier?
If you've bootstrapped out of sample performance for two models, you will obtain an approximation to the sampling distribution of the test statistic (here, the AUC). You can compute then compute the probability that one model's AUC is larger than the other using these samples. Shown below is an example using sklearn
import numpy as np
from sklearn.utils import resample
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.metrics import roc_auc_score
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
%matplotlib inline
X,y=make_classification(n_classes=2, n_samples=1000, n_features=5, random_state=0)
Xtrain, Xval, ytrain, yval = train_test_split(X,y,train_size = 500)
model_1 = LogisticRegression(penalty = 'none', solver='lbfgs').fit(Xtrain, ytrain)
model_2 = LogisticRegressionCV(Cs = [0.004], penalty = 'l1', solver = 'liblinear', max_iter = 1000, cv = 5).fit(Xtrain, ytrain)
model_1_auc = []
model_2_auc = []
for _ in range(1000):
Xvalb, yvalb = resample(Xval, yval)
model_1_p = model_1.predict_proba(Xvalb)[:,1]
model_2_p = model_2.predict_proba(Xvalb)[:,1]
model_1_auc.append(roc_auc_score(yvalb,model_1_p))
model_2_auc.append(roc_auc_score(yvalb,model_2_p))
Here is the result for such a procedure
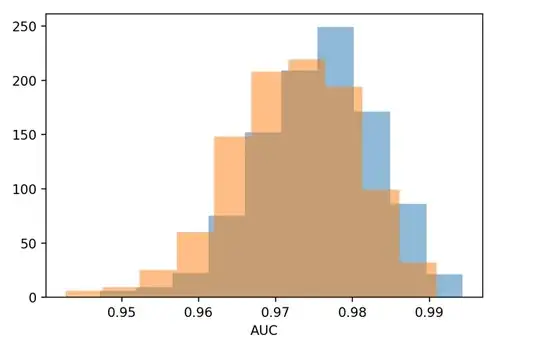
I'm not a big fan of using the term "significant difference" in this case. That makes it sound like you have tested hypothesis about the difference between AUC, and that isn't as easy as it sounds (at least, I don't think it is). What you can do is use these bootstraps to look at the difference between AUCs for each model. You may do something like the following...
diff_in_auc = np.array(model_1_auc)-np.array(model_2_auc)
np.mean(diff_in_auc)
>>>0.00322
So the average difference in the AUC between the two models is on the order of 1e-3. Not a big difference. You could also determine the proportion of the pairs in which model_1 had a larger AUC using similar techniques. I think most people would interpret that as the probability that model_1 has a superior AUC as compared to model 2.
Finally, I would caution you in using AUC as a metric on which to choose models. If I have understood Frank Harrell correctly, the metric isn't sensitive enough to pick up on meaningful improvements between models. EDIT: See this comment by Frank for the fuller story. Thanks to Dave for finding that.
