You can also use the stick-braking process. The story is as follows: imagine that we have a stick and we want to break it into $k$ parts. First you break it into two parts, leave one out, and break the latter again into two parts, repeating this $k-1$ times. Since you always break the remainder, the breakpoints would be ordered.
More formally, the algorithm is described by Frigyik et al (2010) in Introduction to the Dirichlet Distribution and Related Processes:
Step 1: Simulate $u_1 \sim \mathcal{B}(\alpha_1, \sum_{i=2}^k \alpha_i)$, and set $q_1=u_1$. This is the first piece of the stick.
The remaining piece has length $1-u_1$.
Step 2: For $2 \le j \le k-1$, if $j-1$ pieces, with lengths $u_1,u_2,\dots,u_{j-1}$, have been broken off, the length of the
remaining stick is $\prod_{i=1}^{j-1} (1-u_i)$. We simulate $u_j
\sim \mathcal{B}(\alpha_j, \sum_{i=j+1}^k \alpha_i)$ and set $q_j =
u_j \prod_{i=1}^{j-1} (1-u_i)$. The length of the remaining part of
the stick is $\prod_{i=1}^{j-1} (1-u_i) - u_j \prod_{i=1}^{j-1} (1 -
u_i) =\prod_{i=1}^j (1-u_i)$.
Step 3: The length of the remaining piece is $q_k$.
This produces a sample from Dirichlet distribution $\mathbf{q} \sim \mathcal{D}(\boldsymbol{\alpha})$. If you want the distribution to be symmetric, you need $\alpha_1=\alpha_2=\dots=\alpha_k$. Notice that $q_i$'s are the lengths of the sticks, so to mark their borders, you need to take cumulated sum.
Example code:
import numpy as np
import scipy.stats as sp
import matplotlib.pyplot as plt
def stick(α):
k = len(α)
u = sp.beta(a=[α[i] for i in range(0, k-1)],
b=[np.sum(α[i:]) for i in range(1, k)]).rvs(size=k-1)
q = np.zeros(k)
q[0] = u[0]
for i in range(1, k-1):
q[i] = u[i] * np.prod(1 - u[:i])
q[k-1] = np.prod(1 - u[:k])
return q
α = [10, 10, 10, 10]
n_sticks = 25
for s in range(n_sticks):
q = stick(α)
plt.bar(s, q[0], 1)
for i in range(1, len(q)):
plt.bar(s, q[i], 1, bottom=np.sum(q[:i]))
plt.axis('off')
plt.title(f'α = {α}')
plt.show()
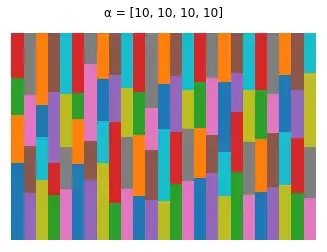
You can manipulate the $\alpha_i$ values, for more details see this answer on parameters of Dirichlet distribution.
Of course, if you have more efficient algorithm for drawing samples from Dirichlet distribution, you can use it and just define the breakpoints as $b_j = \sum_{i=1}^j q_i$.
Other solutions are simpler and computationally less demanding, but this is a stochastic process that you might find interesting, since it seems to share some of the properties of your data.